이전 글 : 2022.08.10 - [데이터/빅데이터분석기사] - [빅데이터분석기사 필기] 3과목 - 빅데이터 모델링 (1/5)
지난 포스트에서는 어떻게 분석모형을 설계하는지에 대해 공부했다. 이번에는 R을 직접 사용하며 구체적인 통계 분석기법을 학습하고자 한다. 이 글은 데이터에듀에서 발행한 '빅데이터 분석기사 필기' 교재 제2권의 48~97페이지에 해당하는 내용을 참고하였다. 학습내용이 많으므로 목차를 사용해 필요한 부분을 찾아가며 공부하기를 권장하는 바이다.
※ 출처가 있는 이미지를 클릭하면 원 사이트로 접속된다.

Index
2장 통계 분석기법
1절 회귀분석
1. 회귀분석의 개념
- 하나 혹은 그 이상의 독립변수가 종속변수에 미치는 영향을 추정해 식으로 표현할 수 있는 통계 기법.
- 변수 사이의 인과관계를 밝히고 모형을 적합해 관심 있는 변수를 예측 or 추론하기위해 사용.
- 1) 적합한 데이터 형태 : 계량형 자료. but 독립변수는 명목척도로 측정된 범주형 자료 가능. (더미변수로 변환)
- 2) 변수 : 설명변수, 독립변수, 예측변수 / 반응변수, 종속변수, 결과변수
- 3) 가정
- 독립, 종속변수 간의 선형성
- 오차의 등분산성 : 오차의 분산은 독립변수의 값과 무관하게 일정해야 함.
- 오차의 정규성 : 오차의 분포가 정규분포를 만족해야 함. 대각방향으로 직선의 형태.
- 오차의 독립성 : 더빈 왓슨 Durbin Watson 검정 실시. 해당 통계량이 2에 가까울수록 자기상관이 없음을 뜻함. (0에 가까우면 양의 상관관계)
- 오차와 잔차 : 오차 - 모집단의 실제값과 회귀분석으로 예측된 값의 차이 / 잔차 - 표본에서 나온 관측값과 회귀분석으로 예측된 값의 차이
2. 단순선형회귀
- 하나의 독립변수가 종속변수에 미치는 영향을 추정할 수 있는 통계기법.
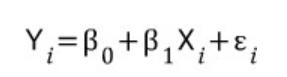
- 회귀식에서 β0, β1을 회귀계수라 함. 회귀분석은 회귀계수를 찾아 독립, 종속변수 간의 함수식을 생성하고, 회귀계수가 유의미한지 파악함.
- 회귀계수 추정방법 : 최소제곱법 - 잔차제곱합 RSS 을 최소로 만드는 직선을 찾는 것
- 결과 해석
- 1) 회귀모형이 통계적으로 유의한가 (F-검정)
- 귀무가설 H0 : 회귀계수가 0이다.
- F-통계량은 회귀모형에 대한 분산분석표로 확인.
- 2) 회귀계수는 통계적으로 유의한가 (t-검정)
- 귀무가설 H0 : i번째 회귀계수가 0이다.
- p-value가 0.05보다 작거나 t-통계량의 절댓값이 2보다 크면 귀무가설 기각.
- 3) 모형은 데이터를 얼마나 설명할 수 있는가 (결정계수 확인)
- 결정계수 (R^2) : 회귀모형이 데이터를 얼마나 잘 설명하는지를 나타내는 척도. 0~1 사이. 1에 가까울수록 높은 설명력.
- 결정계수 = 회귀제곱합 SSR / 총제곱합 SST
- 4) 모형이 데이터를 잘 적합하는가?
- R을 사용한 결과 해석 (p.55)
- 회귀모형의 포뮬러 : lm함수로 회귀모형을 만들고, summary로 결과 요약.
- 모형의 통계적 유의성 검정 : 가장 마지막 줄에서 p-value를 확인. 0.05보다 작음.
- 회귀계수의 유의성 검정 : Coefficients 항목으로 회귀계수 확인. 회귀식 - price = 4.6692 + 5.5629 * EngineSize
- 모형의 설명력 : Adjusted R-squred (수정 결정계수)를 주시. 0.3499이므로 약 35%의 설명력을 지님.
- 모형이 데이터를 잘 적합하는가 : 잔차를 그래프로 표현하고, 회귀진단 실시.
> # data load & check
> library(MASS)
> data("Cars93")
> str(Cars93) #structure
'data.frame': 93 obs. of 27 variables:
$ Manufacturer : Factor w/ 32 levels "Acura","Audi",..: 1 1 2 2 3 4 4 4 4 5 ...
$ Model : Factor w/ 93 levels "100","190E","240",..: 49 56 9 1 6 24 54 74 73 35 ...
$ Type : Factor w/ 6 levels "Compact","Large",..: 4 3 1 3 3 3 2 2 3 2 ...
$ Min.Price : num 12.9 29.2 25.9 30.8 23.7 14.2 19.9 22.6 26.3 33 ...
$ Price : num 15.9 33.9 29.1 37.7 30 15.7 20.8 23.7 26.3 34.7 ...
$ Max.Price : num 18.8 38.7 32.3 44.6 36.2 17.3 21.7 24.9 26.3 36.3 ...
$ MPG.city : int 25 18 20 19 22 22 19 16 19 16 ...
$ MPG.highway : int 31 25 26 26 30 31 28 25 27 25 ...
$ AirBags : Factor w/ 3 levels "Driver & Passenger",..: 3 1 2 1 2 2 2 2 2 2 ...
$ DriveTrain : Factor w/ 3 levels "4WD","Front",..: 2 2 2 2 3 2 2 3 2 2 ...
$ Cylinders : Factor w/ 6 levels "3","4","5","6",..: 2 4 4 4 2 2 4 4 4 5 ...
$ EngineSize : num 1.8 3.2 2.8 2.8 3.5 2.2 3.8 5.7 3.8 4.9 ...
$ Horsepower : int 140 200 172 172 208 110 170 180 170 200 ...
$ RPM : int 6300 5500 5500 5500 5700 5200 4800 4000 4800 4100 ...
$ Rev.per.mile : int 2890 2335 2280 2535 2545 2565 1570 1320 1690 1510 ...
$ Man.trans.avail : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 1 1 1 1 1 ...
$ Fuel.tank.capacity: num 13.2 18 16.9 21.1 21.1 16.4 18 23 18.8 18 ...
$ Passengers : int 5 5 5 6 4 6 6 6 5 6 ...
$ Length : int 177 195 180 193 186 189 200 216 198 206 ...
$ Wheelbase : int 102 115 102 106 109 105 111 116 108 114 ...
$ Width : int 68 71 67 70 69 69 74 78 73 73 ...
$ Turn.circle : int 37 38 37 37 39 41 42 45 41 43 ...
$ Rear.seat.room : num 26.5 30 28 31 27 28 30.5 30.5 26.5 35 ...
$ Luggage.room : int 11 15 14 17 13 16 17 21 14 18 ...
$ Weight : int 2705 3560 3375 3405 3640 2880 3470 4105 3495 3620 ...
$ Origin : Factor w/ 2 levels "USA","non-USA": 2 2 2 2 2 1 1 1 1 1 ...
$ Make : Factor w/ 93 levels "Acura Integra",..: 1 2 4 3 5 6 7 9 8 10 ...
> # simple lenear regression model
> # enginsie : x, price : y
> lm(Price~EngineSize, Cars93)
Call:
lm(formula = Price ~ EngineSize, data = Cars93)
Coefficients:
(Intercept) EngineSize
4.669 5.563
> # model scan : Use summary()
> # summary() : 주어진 인자에 대한 요약정보 제공
> cars93_model <- lm(Price~EngineSize, Cars93)
> summary(cars93_model)
Call:
lm(formula = Price ~ EngineSize, data = Cars93)
Residuals:
Min 1Q Median 3Q Max
-13.684 -4.627 -1.795 2.592 39.429
Coefficients:
Estimate Std. Error t value
(Intercept) 4.6692 2.2390 2.085
EngineSize 5.5629 0.7828 7.107
Pr(>|t|)
(Intercept) 0.0398 *
EngineSize 2.59e-10 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.789 on 91 degrees of freedom
Multiple R-squared: 0.3569, Adjusted R-squared: 0.3499
F-statistic: 50.51 on 1 and 91 DF, p-value: 2.588e-10
> # 그래프 배치
> par(mfrow = c(2,3))
> # 그래프 작성
> plot(cars93_model, which = c(1:6))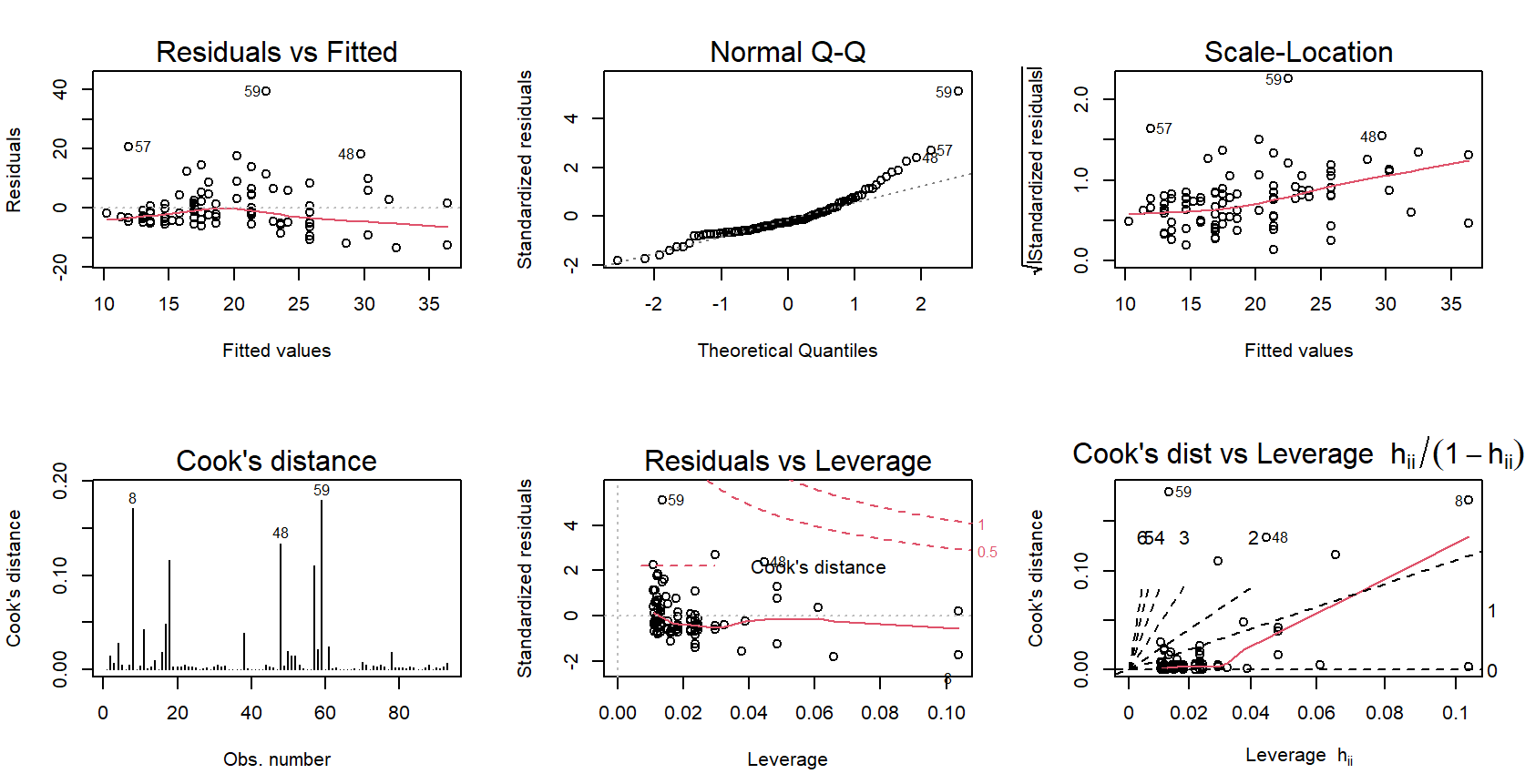
※ 그래프 해석
(1) Residuals vs Fitted : x축 - 회귀모형으로 예측한 y값, y축 - 잔차. 선형회귀모형은 정규성을 가정하기에 오차의 분포는 기울기가 0인 직선의 형태를 나타내야 바람직함.
(2) Normal Q-Q : 표준화된 잔차의 확률도. 정규성 가정 충족 시, 그래프의 점들은 45도의 직선의 형태를 띄어야 함.
(3) Scale-Location : x축 - 회귀모형으로 예측한 y값, y축 - 표준화 잔차. 기울기가 0인 직선의 형태를 나타내야 바람직함. 직선에서 먼 점은 이상치일 가능성이 높음.
(4) Cook's Distance : x축 - 정렬된 관측값, y축 - 해당 위치의 쿡의 거리. 쿡의 거리는 관측치가 회귀모형에 미치는 영향을 나타내는 측도. 1이상이면 크다고 판단.
(5) Residuals vs Leverage : x축 - 레버리지, y축 - 표준화 잔차. 레버리지는 관측값이 다른 관측값 집단으로부터 떨어진 정도이자 설명변수가 극단에 치우친 정도를 의미. 쿡의 거리가 0.5이상인 빨간 점선의 범위 밖에 있는 점은 이상치로 볼 수 있음.
(6) Cook's dist vs Leverage : x축 - 레버리지, y축 - 쿡의 거리. 레버리지와 쿡의 거리는 비례함.
3. 다중선형회귀
- 다중선형회귀분석 : 복수의 독립변수가 종속변수에 미치는 여향을 추정하는 통계기법.
- 여러 독립변수가 사용된 회귀식 생성.
- 중선형회귀분석 or 다변량 회귀분석이라고도 함.
- 검토사항
- 1) 데이터가 가정을 만족하는가?
- 독립변수와 종속변수의 선형성, 오차의 독립성/등분산성/정규성을 만족해야 함.
- 2) 다중공선성 Multicollinearity
- 다중공선성 : 회귀분석에서 독립변수 사이에 강한 상관관계로 인해 발생하는 문제. PCA나 릿지 회귀모형 등으로 문제 해결.
- 다중공선성 검사 방법
- (1) 독립변수 간의 상관계수를 직접 구함
- (2) 허용오차가 0.1이하이면 다중공선성 문제가 심각.
- 허용오차 : 독립변수의 분산 중 다른 독립변수에 의해 설명되지 않는 부분. 0~1사이의 값.
- (3) 분산팽창요인 VIF (허용오차의 역수)가 10이상인지 확인.
- 결과 해석
- 1) 회귀모형이 통계적으로 유의한가 (F-검정)
- 귀무가설 H0 : 회귀계수가 0이다.
- F-통계량은 회귀모형에 대한 분산분석표로 확인.
- 2) 회귀계수는 통계적으로 유의한가 (t-검정)
- 귀무가설 H0 : i번째 회귀계수가 0이다.
- p-value가 0.05보다 작거나 t-통계량의 절댓값이 2보다 크면 귀무가설 기각.
- 독립변수의 영향력에 대한 비교는 표준화된 계수로 살펴봐야 함.
- 표준화된 계수 : 입력 데이터를 평균이 0, 표준편차가 1이 되도록 만든 데이터로 분석했을 때의 회귀계수.
- 3) 모형은 데이터를 얼마나 설명할 수 있는가 (결정계수 확인)
- 결정계수 (R^2) : 회귀모형이 데이터를 얼마나 잘 설명하는지를 나타내는 척도. 0~1 사이. 1에 가까울수록 높은 설명력.
- 결정계수 = 회귀제곱합 SSR / 총제곱합 SST
- 독립변수의 유의성과 무관하게 독립변수의 수가 많아지면 결정계수가 커짐. 따라서, 수정된 결정계수를 활용함.
- 4) 모형이 데이터를 잘 적합하는가?
- R을 사용한 결과 해석 (p.62)
- 회귀모형의 포뮬러 : Price가 종속변수, 나머지 3개의 독립변수
- 모형의 통계적 유의성 검정 : F-통계량 - 37.98 / p-value < 0.05 이므로 유의함
- 회귀계수의 유의성 검정 : Coefficient 항목에서 모든 p-value가 0.05보다 작음.
- 모형의 설명력 : 수정된 결정계수 - 0.5467.
> # load data
> library(MASS)
> str(Cars93)
'data.frame': 93 obs. of 27 variables:
$ Manufacturer : Factor w/ 32 levels "Acura","Audi",..: 1 1 2 2 3 4 4 4 4 5 ...
$ Model : Factor w/ 93 levels "100","190E","240",..: 49 56 9 1 6 24 54 74 73 35 ...
$ Type : Factor w/ 6 levels "Compact","Large",..: 4 3 1 3 3 3 2 2 3 2 ...
$ Min.Price : num 12.9 29.2 25.9 30.8 23.7 14.2 19.9 22.6 26.3 33 ...
$ Price : num 15.9 33.9 29.1 37.7 30 15.7 20.8 23.7 26.3 34.7 ...
$ Max.Price : num 18.8 38.7 32.3 44.6 36.2 17.3 21.7 24.9 26.3 36.3 ...
$ MPG.city : int 25 18 20 19 22 22 19 16 19 16 ...
$ MPG.highway : int 31 25 26 26 30 31 28 25 27 25 ...
$ AirBags : Factor w/ 3 levels "Driver & Passenger",..: 3 1 2 1 2 2 2 2 2 2 ...
$ DriveTrain : Factor w/ 3 levels "4WD","Front",..: 2 2 2 2 3 2 2 3 2 2 ...
$ Cylinders : Factor w/ 6 levels "3","4","5","6",..: 2 4 4 4 2 2 4 4 4 5 ...
$ EngineSize : num 1.8 3.2 2.8 2.8 3.5 2.2 3.8 5.7 3.8 4.9 ...
$ Horsepower : int 140 200 172 172 208 110 170 180 170 200 ...
$ RPM : int 6300 5500 5500 5500 5700 5200 4800 4000 4800 4100 ...
$ Rev.per.mile : int 2890 2335 2280 2535 2545 2565 1570 1320 1690 1510 ...
$ Man.trans.avail : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 1 1 1 1 1 ...
$ Fuel.tank.capacity: num 13.2 18 16.9 21.1 21.1 16.4 18 23 18.8 18 ...
$ Passengers : int 5 5 5 6 4 6 6 6 5 6 ...
$ Length : int 177 195 180 193 186 189 200 216 198 206 ...
$ Wheelbase : int 102 115 102 106 109 105 111 116 108 114 ...
$ Width : int 68 71 67 70 69 69 74 78 73 73 ...
$ Turn.circle : int 37 38 37 37 39 41 42 45 41 43 ...
$ Rear.seat.room : num 26.5 30 28 31 27 28 30.5 30.5 26.5 35 ...
$ Luggage.room : int 11 15 14 17 13 16 17 21 14 18 ...
$ Weight : int 2705 3560 3375 3405 3640 2880 3470 4105 3495 3620 ...
$ Origin : Factor w/ 2 levels "USA","non-USA": 2 2 2 2 2 1 1 1 1 1 ...
$ Make : Factor w/ 93 levels "Acura Integra",..: 1 2 4 3 5 6 7 9 8 10 ...
> # multiple regression model
> price_lm <- lm(Price~EngineSize + RPM + Weight, Cars93)
> summary(price_lm)
Call:
lm(formula = Price ~ EngineSize + RPM + Weight, data = Cars93)
Residuals:
Min 1Q Median 3Q Max
-10.511 -3.806 -0.300 1.447 35.255
Coefficients:
Estimate Std. Error t value
(Intercept) -51.793292 9.106309 -5.688
EngineSize 4.305387 1.324961 3.249
RPM 0.007096 0.001363 5.208
Weight 0.007271 0.002157 3.372
Pr(>|t|)
(Intercept) 1.62e-07 ***
EngineSize 0.00163 **
RPM 1.22e-06 ***
Weight 0.00111 **
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05
‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.504 on 89 degrees of freedom
Multiple R-squared: 0.5614, Adjusted R-squared: 0.5467
F-statistic: 37.98 on 3 and 89 DF, p-value: 6.746e-16
- 최적 회귀방정식 선택
- 1) 단계적 변수선택 : 전진 선택법 (절편만 있는 상수모형에서 시작해 설명변수를 모형에 추가), 후진 제거법, 단계적 방법
- 2) 벌점화된 선택기준
- AIC (Akaike Information Criterion) : 최소의 정보 손실을 갖는 모델을 적합하다고 판단.
- BIC (Bayesian Information Criterion) : AIC와 비슷. 변수가 많을수록 페널티 부여
- 3) 수정된 결정계수 : MSE값이 최소인 시점의 모형을 선택 or 최소와 비슷해 변수를 추가하지 않아도 되는 시점의 모형 선택
- 4) Mallows's Cp : 모든 변수를 사용한 모형과 p개의 독립변수를 사용한 모형이 얼마나 가까운지 나타내는 통계량. 작을수록 좋음.
- 대개 모델에 변수가 추가될수록 잔차제곱합이 작아짐. 잔차제곱함이 작은 모델을 선택하면, 모든 변수를 포함하는 모델일 가능성이 높고, 이는 과적합의 발생으로 이어질 수 있음.
4. 정규화 선형회귀
- 정규화 선형회귀 : 선형회귀계수에 제약조건을 추가하여 오버피팅을 막는 방법.
- 릿지 회귀 : 가중치의 제곱합을 최소화하는 것이 제약조건.
- 가중치의 모든 원소가 0에 가까워지길 원함. 규제방식 - L2 penalty
- 람다 λ는 기존의 잔차제곱합과 추가된 제약조건의 비중을 조절하기 위한 하이퍼 파라미터. 람다가 커지면 가중치가 줄어들고 정규화 정도가 커짐. 람다가 0일 땐, 일반적 선형회귀 모형이 됨.
- 라쏘 회귀 : 가중치 절대값의 합을 최소화는 것이 제약조건
- 가중치가 0에 가까워지나 0이 되지 않는 릿지 회귀와 달리 라쏘는 가능함.
- L1 penalty 사용.
- 엘라스틱 넷 Elastic Net : 릿지 + 라쏘. 두 개의 하이퍼 파라미터를 지님.
5. 일반화 선형회귀 GLM
- 회귀분석은 정규성을 전제로 하지만, 종속변수가 범주형 or 만족하지 못할 때도 있음. 이 경우, 종속변수를 적절한 함수로 바꿔 독립변수와 선형 결합으로 모형화하는 일반화 선형모형을 활용함.
- 랜덤성분 (종속변수의 확률분포 규정), 체계적 성분 (y의 기댓값을 정의하는 설명변수 사이의 선형 결합), 연결함수 (랜덤성분과 체계적 성분 연결)의 3가지 성분으로 정의.
6. 회귀분석의 영향력 진단
- 회귀모형의 안전성을 판단하는 통계 기법.
- 특정 관측값이 제외되며 변동이 클수록 안전성이 약하다고 판단.
- 영향점 : 회귀직선의 기울기에 영향을 크게 미치는 점.
- Cook's Distance, DFBEtAS, DFFItS, Leverage H 등 활용.
2절 범주형 자료 분석
1. 범주형 자료 분석
- 설명변수 : 범주형 / 반응변수 : 범주형 ☞ 분할표 분석, 카이제곱 검정
- 설명변수 : 범주형 / 반응변수 : 연속형 ☞ T-검정, 분산분석
- 설명변수 : 연속형 / 반응변수 : 범주형 ☞ 로지스틱 회귀분석
2. 분할표 분석 Contingency Table
- 분할표 (교차표) : 복수의 범주형 변수를 기준으로 빈도를 표 형태로 나타낸 것. (1원, 2원, 다원 분할표)
- 행은 설명변수, 열은 반응변수.
- 상대위험도 : 관심 집단의 위험률 / 비교집단의 위험률. 위험률은 특정 사건이 발생할 비율.
- 오즈비 Odds Ratio : 성공확률 / 실패확률. 오즈는 각 범주별 비율
3. 교차분석
- 카이제곱 검정 : 범주형 자료 (명목, 서열)인 두 변수의 관계를 알아보고자 실시하는 분석 기법.
- 적합성 검정, 독립성 검정, 동질성 검정에 활용되고 카이제곱 검정 통계량을 사용함.
- 교차표 : 두 변수의 각 범주를 교차해 데이터의 빈도를 표 형태로 나타낸 것.
- 교차분석은 교차표에서 각 셀의 관찰빈도와 기대빈도 (이론적으로 기대할 수 있는 빈도분포) 간의 차이를 검정.
4. 적합성 검정
- 적합성 검정 : 실험에서 얻어진 관측값이 예상한 이론과 일치하는지 검정하는 방법. 모집단 분포에 대한 가정이 옳은지 관측자료와 비교하여 검정하는 것.
- 가설 설정
- n개의 표본을 k개의 범주로 나누고 각 범주의 곽측도수와 주어진 확률 분포에 대해 각 범주에 속하는 기대도수가 적합한지 검정.
- 귀무가설 H0 :실제 분포와 이론적 분포 사이에는 차이가 없다.
- 검정통계량
- O : 관찰도수, E : 기대도수.
- 검정통계량 값이 큰 경우 : 관찰도수와 기대도수의 차이가 크며 적합도가 낮음. 일치로 보기 어려움.
- 자유도
- df = k-1
- k = 범주의 개수
5. 독립성 검정
- 독립성 검정 : 모집단이 두 변수에 의해 범주화됐을 때, 두 변수가 독립인지 검정하는 것. 교차표 활용.
- 독립 : 한 사건이 다른 사건이 일어날 확률에 영향을 주지 않는 것. P(A∩B) = P(A) * P(B)
- 가설 설정
- 모집단을 범주화하는 기준이 되는 두 변수가 독립적으로 영향을 주는지 여부를 검정.
- 귀무가설 H0 : 두 변수 간에는 연관이 없다.
- 검정 통계량
- 통계량이 큰 경우 : 두 변수 사이에 연관관계가 있음.
- 자유도
- df = (R-1)(C-1) / R : 행의 수, C : 열의 수
6. 동질성 검정
- 모집단이 임의의 변수에 의해 R개의 속성으로 범주화됐을 때, R개의 부분 모집단에서 추출한 표본 C개의 범주화된 집단의 분포가 서로 동일한지 검정하는 것
- 통계량 계산 시, 교차표 활용. 계산법, 검증법은 독립성 검정과 동일
- 가설설정
- j= 1, 2, ~ c
- 귀무가설 : 모든 P는 동일.
- 검정통계량
- 통계량 값이 큰 경우 : P중 다른 값이 존재한다.
- 자유도 : df = (R-1)(C-1)
3절 다차원척도법 Multimensional Scailing
1. 다차원 척도법
- 객체 간 근접성 proximity을 시각화하는 통계 기법.
- 유사성, 비유사성을 측정해 2차원, 3차원 공간에 점으로 표현해 시각화.
2. 다차원 척도법의 목적
- 데이터 속에 숨은 패턴, 구조를 찾는다.
- 찾아낸 구조를 소수 차원의 공간에 기하학적으로 표현.
- 데이터 축소 Data Reduction
3. 분석 방법
- 유클리드 거리행렬을 사용해 거리 계산.
- 상대적 거리 정확도를 제고하고자 스트레스 값으로 적합 정도를 나타냄.
- 각 개체를 공간 상에 표현하기 위한 방법은 부적합도 기준. STRESS, S-STRESS 사용. (STRESS - 0 : 완벽, 0.15 이상 : 나쁨)
- 최적모형의 적합 : 부적합도를 최소로하는 반복 알고리즘. 이 값이 일정 수준 이하일 때 적합 모형으로 선정.
4. 다차원 척도법의 종류
- 계량적 MDS : 데이터가 구간척도 or 비율척도일 때. N개의 케이스에 대해 p개의 특성변수가 있다면, 각 개체들 사이의 유클리드 거리행렬을 계산, 비유사성 S (거리제곱 행렬의 선형함수)를 공간에 표현.
> library(MASS)
> cmd <- cmdscale(eurodist)
> x <- cmd[, 1]
> y <- -cmd[, 2] # 북쪽 도시의 상단 표기를 위해 부호 변환
> plot(x, y, type = "n", asp=1,
+ main = "Metric MDS")
> text(x,y, rownames(cmd), cex = 0.6)
> abline(v = 0, h =0, lty = 2, lwd = 0.7)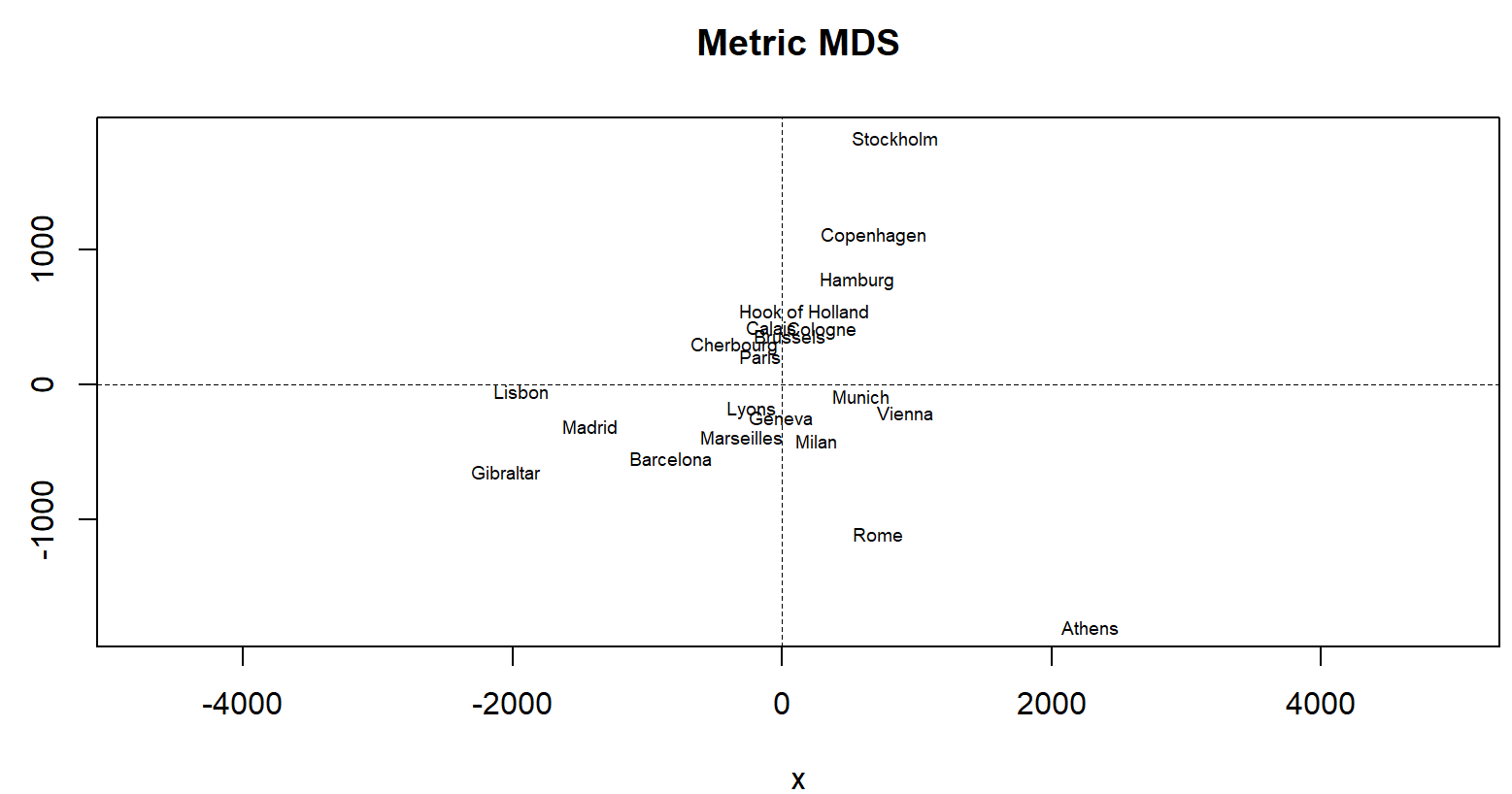
- 비계량적 MDS Non-Metric MDS : 데이터 - 순서척도. 개체 사이의 거리가 순서로 주어졌다면, 순서척도를 거리 속성과 동일하게 변환하여 거리 생성 후 적용.
- isoMDS 예시
> library(MASS) # 데이터 패키지
> data(swiss)
> swiss_land <- as.matrix(swiss[,-1])
> swiss.dist <- dist(swiss_land)
> swiss.mds <- isoMDS(swiss.dist)
initial value 2.979731
iter 5 value 2.431486
iter 10 value 2.343353
final value 2.338839
converged
> plot(swiss.mds$points, type = "n")
> text(swiss.mds$points,
+ labels = as.character(1:nrow(swiss_land)))
> abline(v = 0, h = 0, lty= 2, lwd =0.5)

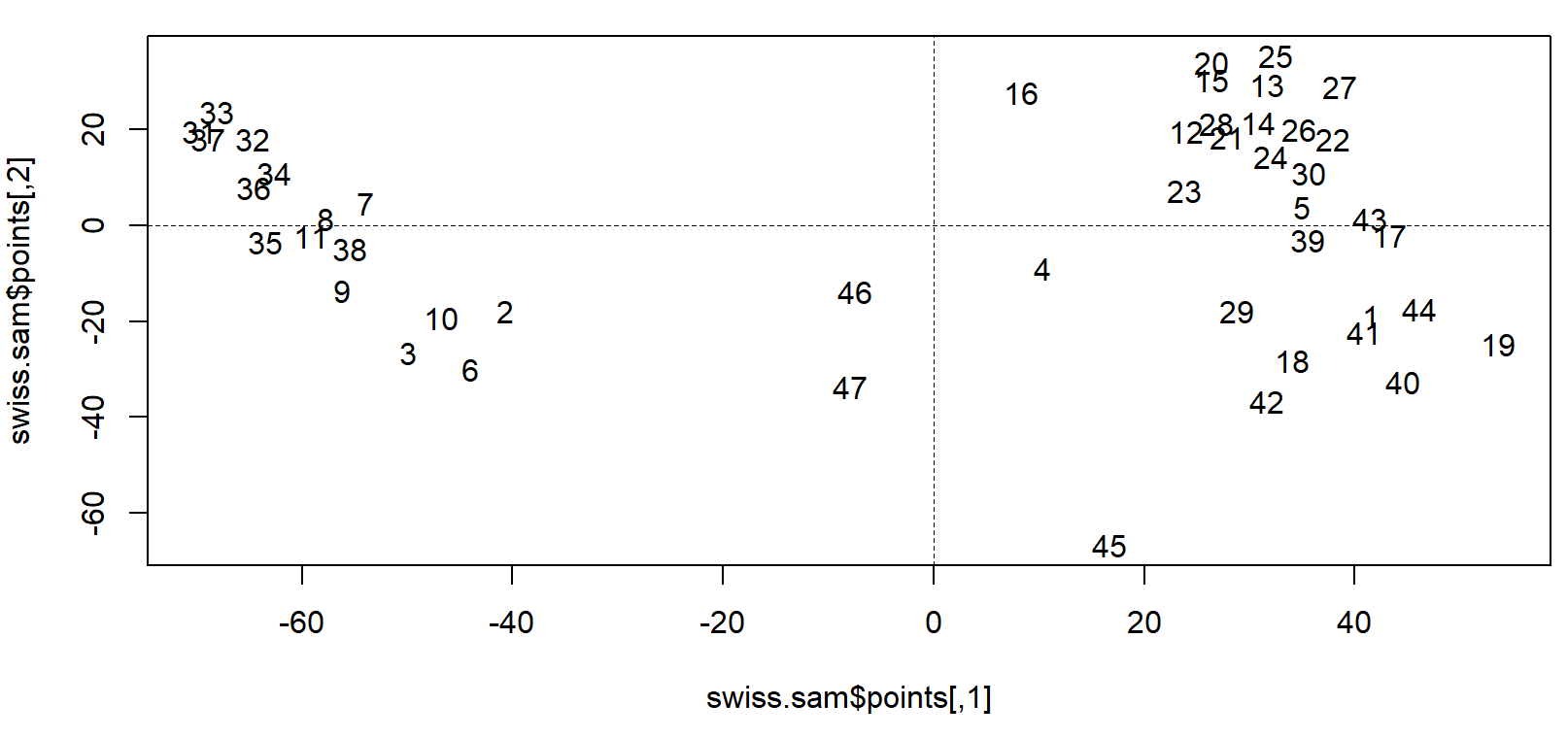
- sammon 예시
> # sammon
> swiss.sam <- sammon(swiss.dist)
Initial stress : 0.00824
stress after 10 iters: 0.00439, magic = 0.338
stress after 20 iters: 0.00383, magic = 0.500
stress after 30 iters: 0.00383, magic = 0.500
> plot(swiss.sam$points, type = "n")
> text(swiss.sam$points,
+ labels = as.character(1:nrow(swiss_land)))
> abline(v = 0, h = 0, lty= 2, lwd =0.5)
4절 다변량 분석 Multivariate Analysis
1. 주성분 분석 PCA
- 주성분 분석 : 서로 상관성이 높은 변수의 선형결합으로 이뤄진 주성분이라는 새로운 변수를 만들어 요약 및 축소하는 기법
- 첫번째 주성분으로 전체 변화를 가장 많이 설명
- 주성분은 서로 독립이어야 함.
- 주성분 분석의 목적
- 소수의 주성분으로 차원 축소
- 다중공선성 존재 시, 상관성 없는 주성분으로 변수 축소하여 모델 활용 가능
- 군집분석 시, 연산속도 향상.
- 주성분 선택
- 1) 기여율 : 원 변수의 총 변동 (각 변수의 분산값 합계) 분의 주성분 변수의 분산. 총변동에 대한 주성분의 설명력 의미.
- 주성분 분산이 전체 데이터의 분산과 비슷하면 해당 주성분은 적절. 기여율은 1에 가까울수록 바람직함.
- 누적 기여율이 85% 이상이면 해당 지점까지를 주성분의 수로 함.
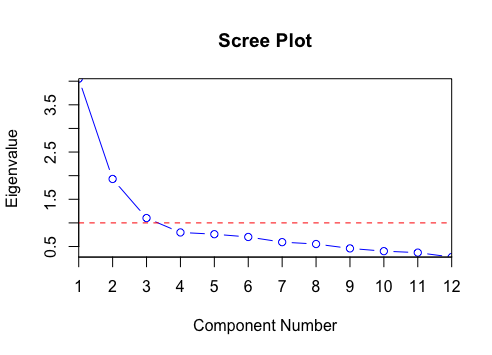
- 2) 스크리 산점도 Scree Plot : x축 - 주성분, y축 : 주성분의 고윳값(분산)인 그래프.
- 고유치가 급격히 완만해지는 지점의 직전 단계까지 주성분의 수를 선택. (3부터 완만해지므로 2선택)
2. 요인분석 Factor Analysis
- 요인분석 : 변수 간의 상관관계를 감안해 서로 비슷한 변수를 묶어 새로운 잠재요인을 추출하는 방법.
- 변수가 간격 혹은 비율척도. 표본은 100개 이상 (최소 50개 이상)
- 주성분분석과의 비교. (추가 예정)
- 용어
- 요인 적재값 : 변수와 해당 요인의 상관계수. 요인 적재값의 제곱은 해당 변수가 요인으로 설명되는 분산의 비율.
- 고윳값 Eigenvalue : 각 요인에 대한 모든 변수의 요인 적재값 제곱의 합. 해당 요인이 설명할 수 있는 변수의 분산의 총합.
- 공통성 : 여러 요인이 설명할 수 잇는 한 변수의 분산의 양을 백분율로 표시한 것. 한 변수의 공통성은 추출된 요인이 그 변수의 정보(분산)을 얼마나 설명하는지를 뜻함.
- 요인 추출 방법
- 주성분분석 : 전체 분산을 바탕으로 요인 추출. 주로 사용됨.
- 공통요인분석 : 잠재요인에서 변수가 산출된 것으로 보는 방식. 공통분산만으로 요인 추출.
- 요인의 수 결정
- 고윳값을 기준일 때 : 고윳값이 1이상인 요인 추출.
- 스크리 도표 : 기울기가 꺾이는 지점 유의.
- 요인분석 절차 : 데이터 입력 - 상관계수 산출 - 요인 추출 - 요인 적재량 산출 - 요인 회전 (직각 회전 or 비직각 회전) - 생성된 요인 해석 - 요인점수 (요인점수 계수 * 표준화된 관측치) 산출
3. 판별분석 Discriminant Analysis
- 판별분석 : 집단에 대한 정보로 집단을 구별할 수 있는 판별함수 또는 판별규칙을 만들고 새로운 개체가 어느 집단에 속하는지 판별해 분류하는 다변량 기법.
- 독립변수 : 간격척도 or 비율척도 / 종속변수 : 명목척도 or 서열척도
- 종속변수의 집단 수가 3개 이상이면 다중판별분석.
- 판별식 도출
- 그룹 내 분산에 비해 그룹 간 분산의 차이를 최대화하는 독립변수의 계수를 탐색.
- 판별함수는 '집단의 수 - 1', '독립변수의 수' 중 더 작은 값만큼 생성됨. 가장 먼저 계산된 판별식의 판별력이 가장 높음.
- 가정
- 독립변수는 다변량 정규분포.
- 종속변수에 의해 범주화되는 그룹의 분산-공분산행렬이 동일
- 판별함수에 포함될 독립변수의 선택 방법 : 동시입력방식, 단계입력방식
- 적합도 평가
- Wilk's lambda 값을 활용해 카이제곱 검증 실시.
- overall fit 점검을 위해 hit ratio 확인. (hit ratio : 정확히 분류된 대상의 수 / 전체 대상의 수)
5절 시계열 분석
1. 시계열 자료
- 시계열 자료 : 시간의 흐름에 따라 관측된 자료.
- 종류 : 비정상성 시계열 자료, 정상성 시계열 자료
2. 정상성
- 정상성 : 시계열의 확률적인 성질이 시간의 흐름에 따라 변하지 않는 것. 시계열 분석을 진행하기 위해서는 정상성을 만족해야 함.
- 조건
- 평균이 일정 : 평균이 일정하지 않은 경우엔 차분 (현시점 자료에서 전 시점 자료를 빼는 것)으로 정상화.
- 분산이 일정 : 분산이 일정하지 않다면 변환으로 정상화.
- 공분산은 시차에만 의존. 특정 시점에 의존하지 않는다.
- 정상시계열의 특징
- 어떤 시점에서 평균, 분산, 특정 시차의 길이를 갖는 자기공분산을 측정해도 동일 값을 지님.
- 항상 평균값으로 회귀하려는 경향. 평균값 주변에서의 변동폭은 일정
3. 시계열 자료 분석방법
- 분석방법 : 회귀분석, Box-Jenkins, 지수평활법, 시계열 분해법
- 자료 형태별 분석방법
- 일변량 : Box-Jenkins(ARMA), 지수평활법, 시계열 분해법 등
- 다변량 : 회귀분석(계량경제), 전이함수 모형, 개입분석 등
- 이동평균법 Moving Average Method
- 개념 : 과거부터 현재까지의 자료를 대상으로 일정기간별 이동평균을 계산하고 추세를 파악해 다음 기간을 예측하는 방법. 계절변동과 불규칙변동을 제거해 추세변동과 순환변동만 가진 시계열로 변환하는 방법이기도 함.
- 특징
- 1) 간단. 자료 수가 많고 안정적 패턴을 보이면 예측 품질이 높음.
- 2) 특정 기간에 속하는 시계열은 동일 가중치.
- 3) 불규칙 변동이 심하지 않은 경우 짧은 기간의 평균 사용.
- 4) 적절한 기간, 즉, 적절한 m의 개수를 선정하는 것이 가장 중요
- 지수평활법 Exponential Smooting Method
- 모든 시계열 자료를 사용해 평균을 구하고, 최근 데이터에 더 많은 가중치를 부여해 미래 예측.
- 특징
- 1) 단기간에 발생하는 불규칙변동을 평활하는 방법.
- 2) 지수평활계수가 가중치 역할을 하며, 불규칙변동이 큰 시계열의 경우 낮은 지수평활계수를 가짐. (일반적으로 0.05~0.3)
- 3) 지수평활계수는 예측오차 (실제 관측값과 예측값 사이의 잔차제곱합)를 비교해 예측오차가 작은 값을 고르는 것이 이상적.
- 4) 지수평활계수는 과거일수록 감소.
- 5) 중기 예측 이상에 주로 사용.
4. 시계열 모형
- 자기회귀 모형 (AR 모형)
- 자기상관성 : p 시점 전의 자료가 현재 자료에 영향을 주는 것. 자귀회귀 모형은 자기 상관성을 시계열 모형으로 나타낸 것.
- 자기상관함수 ACF : 시계열 데이터의 자기상관성을 파악하기 위한 함수
- 이동평균 모형 (MA 모형)
- 시간이 지날수록 관측치의 평균값이 지속적으로 증가하거나 감소하는 경향을 나타낸 시계열 모형.
- 현시점의 자료를 유한한 수량의 백색잡음의 결합으로 표현해 늘 정상성 만족.
- 자기회귀누적이동평균 모형 (ARIMA 모형)
- 자기회귀와 이동평균을 모두 고려. 과거값과 과거 예측오차로 현재값을 설명.
- ARIMA 모형은 비정상 시계열 모형. 차분이나 변환으로 다른 모형으로 정상화 가능.
- ARIMA 모형은 p, d, q의 3개 차수가 있음. d - 차분의 횟수, p - AR모형 지수, q - MA모형 지수
- 분해 시계열
- 시계열에 영향을 주는 일반적 요인을 시계열에서 분리해 분석하는 방법.
- Z = f(T, S, C, I)
- T : 경향요인, S : 계절요인, C : 순환요인, I : 불규칙요인
6절 비모수 통계
1. 개요
- 모수적 방법 : 모집단의 분포에 대한 가정 ▶ 검정통계량과 검정통계량의 분포를 유도해 검정.
- 비모수적 방법 : 추출된 모집단 분포에 아무 제약을 가하지 않고 검정. 특정 분포를 따른다고 할 수 없는 경우에 활용.
2. Kolmogorov-Smirnov 검정 (단일 표본)
- 단일표본 Kolmogorov-Smirnov 검정은 관측치들이 정규분포, 포아송분포 등과 같은 특정 분포를 따르는지 검정하는 방법.
- 누적관측분포와 누적이론적 분포와의 가장 큰 차이 (절대값)에서 검정통계량 계산.
- 조건 : 데이터는 순위자료 이상, 연소적 분포를 가정.
- 가설 : 귀무가설 H0 - 주어진 자료는 ??분포를 따른다. (검정통계량 Z가 작을수록 귀무가설 기각 어려움)
3. Mann-Whitney U 검정 (독립 두 표본)
- Mann-Whitney U 검정은 두 집단의 분포가 동일한지 살펴보는 방법.
- 두 집단의 관측값을 통합해 크기 순으로 정렬 후 순위 부여. 그룹별로 순위의 합을 구해 두 그룹의 순위합 크기가 통계적으로 차이가 있는 검정하는 방법.
- Wilcoxon rank-sum 검정은 순위합을 활용한는 검정법이고, 검정통계량은 다르나 결과는 동일.
- 독립인 두 집단의 평균 차이를 비교하려고 할 때 (정규성 만족) : 모수적 방법 - 독립표본 t-검정
- 독립인 두 집단의 평균 차이를 비교하려고 할 때 (정규성 불만족) : 비모수적 방법 - Mann-Whitney U 검정 or Wilcoxon rank-sum 검정
- 가설 : 귀무가설 - 두 집단의 순위합은 동일.
4. 윌콕슨의 부호 순위 검정 Wilcoxon rank-sum test (대응 두 표본)
- 대응하는 두 중위수에 차이가 있는지 검정.
- 쌍을 이루는 두 집단의 평균 차이를 비교하려고 할 때 (정규성 만족) : 모수적 방법 - 대응표본 t-검정
- 쌍을 이루는 두 집단의 평균 차이를 비교하려고 할 때 (정규성 불만족) : 비모수적 방법 - Wilcoxon rank-sum 검정
- 가설 : 귀무가설 - 두 집단의 중앙값은 동일.
5. 런 검정 Run test
- 연속적인 관측값들이 무작위로 나타났는지 검정하는 방법. 우연성 검정이라고도 함.
- 런 : 한 종류의 부호 또는 집단이 시작하여 끝날 때까지의 덩어리. A sequence of like observations
- 양의 상관이라면, 이전 시점의 값이 지속되는 경향.
- 표본이 독립적? 중앙선을 기준으로 런이 교차하는 경우가 매우 적거나 많다면, 독립적이라고 보기 어려움.
- 표본의 크기가 n, 런의 수가 R, 표본이 독립일 때, R은 정규분포.
- 가설 : 일련의 관측치는 랜덤 (표본은 독립)
♧ 예상문제 오답 정리
- 주성분분석은 변수선택용이 아님.
- 결정계수는 총 변동 중에서 회귀모형에 의해 설명되는 변동이 차지하는 비율.
- 회귀식에 대한 검정은 회귀계수 (독립변수의 기울기)가 0 - 귀무가설, 0이 아님 - 대립가설로 설정.
- 오차의 정규성 확인 방법
- Q-Q plot
- 히스토그램
- Shapiro-Wilks Test
- 더빈 왓슨은 오차항의 자기상관 여부 파악.
- 영향력 진단 (안정성 평가) - DFFITS : 절대값이 기준치보다 클 때, 높은 영향력을 지닌다고 간주.
- 후진제거법 : p-value가 높은 독립변수부터 제거
- 최적회귀방정식 - 단계적 방법 : 예측 변수의 추가, 제거를 반복하는데 전진, 후진선택과 동일한 모형을 취하지 않음.
- 정상성 : 분산이 시점에 의존하지 않음.
- d번 차분 → ARMA(p,q) 일 때, ARIMA(p,d,q).
- 순환변동 : 경제적, 자연적 이유없이 미지의 주기로 변화하는 것
- 계절변동 : 짧은 기간 동안의 주기적 패턴
- 시계열분석 모델링 - 데이터 기반 : 데이터 패턴이 자주 바뀔 때 유용. 계산량 많지 않음. 단순이동평균법은 추세와 계절성이 없을 때 적합.
- 시계열 데이터 분석 절차
- 1) 시간 그래프 작성
- 2) 추세와 계절성 제거
- 3) 잔차 예측
- 4) 잔차에 대한 모델 적합
- 5) 예측된 잔차에 추세와 계절성을 고려하여 데이터 예측
- 다변량 분석으로 4차원 이상의 데이터를 표현하기 어렵기에 3차원 공간을 확장하는 기법으로 나타냄.
- 차원축소 기법 - 주성분분석, 요인분석, 다차원 척도법, 독립성분 분석, 특이값 분해
- 제1주성분 : 변동을 최대로 설명해주는 방향으로 변수를 선형결합.
- R코드 princomp(data, cor = True) 이므로 상관행렬 사용.
- 주성분분석으로 변수 사이의 구조를 이해하는 것은 쉽지 않음.
- biplot
- 화살표 : 원 변수와 주성분 간의 상관계수.
- 화살표의 길이 : 분산 (길수록 분산 큼)
- 주성분개수 선택 방법 - 평균 고윳값 : 고윳값의 평균을 구하고 평균 이상이 되는 주성분 설정.
- 주성분분석으로 생성된 변수는 원 변수와의 선형결합으로 생성됨.
- 요인분석은 목표변수를 고려치 않고, 비슷한 유형의 변수를 묶어 새 변수 창출.
- 비모수 검정 방법 - 부호 검정 sign test : 표본들이 관련있는 경우, 짝지어진 두 관찰치의 대소를 표시하며 그 개수로 분포의 차이가 있는지 가설을 검정하는 방법.
'Cerificate > 빅데이터분석기사' 카테고리의 다른 글
| [빅데이터분석기사 필기] 3과목 - 빅데이터 모델링 (4/5) (0) | 2022.08.17 |
|---|---|
| [빅데이터분석기사 필기] 3과목 - 빅데이터 모델링 (3/5) (0) | 2022.08.14 |
| [빅데이터분석기사 필기] 3과목 - 빅데이터 모델링 (1/5) (0) | 2022.08.10 |
| [빅데이터분석기사 필기] 2과목 - 빅데이터 탐색 (3/3) (어려움) (0) | 2022.08.09 |
| [빅데이터분석기사 필기] 2과목 - 빅데이터 탐색 (2/3) (0) | 2022.08.07 |





