728x90
반응형
지난 포스트에서는 여러 통계 분석기법을 공부했다. 이번에는 정형 데이터를 분석하는 방법을 배우고자 한다. 전과 마찬가지로 R을 사용한 예제가 같이 올라갈 것이다. 이 글은 데이터에듀에서 발행한 '빅데이터 분석기사 필기' 교재 제2권의 122~161페이지에 해당하는 내용을 참고하였다.
※ 출처가 있는 이미지를 클릭하면 원 사이트로 접속된다.

Index
3장 정형 데이터 분석기법
1절 분류분석
1. 로지스틱 회귀분석
- 반응변수 (종속변수)가 범주형일 때 사용하는 회귀분석 모형. 반응변수가 특정 그룹에 속할 확률은 0~1로 예측. 예측 확률에 따라 가능성이 높은 그룹으로 분류하는 지도학습 알고리즘.
- 원리
- 반응변수 Y가 범주형일 때, 일반적 선형회귀모형으로는 값을 바로 추정할 수 없음. Y는 0과 1로 구성된 이진형 반응변수이나, 우변의 식은 무한대의 값을 가지기 때문.
- 로지스틱 회귀분석에서는 범주형 변수 Y도 무한대의 값을 지니도록 로짓변환 실시.
- 오즈 odds : 사건의 실패확률에 대한 성공확률의 비. 0~무한대 사이의 값을 지님.
- 로그 오즈 : 오즈에 로그함수를 적용한 것. -무한대~+무한대의 값. 로짓변환 - 범주형 반응변수를 로그 오즈로 변환하는 것.
- 시그모이드 함수 (확률 계산) : 로그 오즈값을 0~1 사이의 값으로 바꿔 성공 여부를 알 수 있게 해주는 함수. 확률 P에 대해 식을 정리해야 함.
- 임계값 : 데이터가 어떤 그룹에 속하는지 분류의 기준이 되는 값. 일반적으로 0.5지만, 병원 진단에서는 임계값을 낮춰 민감도를 높일 수 있음.
- R을 이용한 로지스틱 회귀분석
- p-value가 0.05보다 큰 변수가 많아 step함수로 단계적선택법을 활용해 로지스틱 재시도
- 20개 독립변수 중 13개 변수 선정. ('*', '.'으로 표시됨)
- estimate가 양수일 때, 독립변수가 1 증가하면 확률이 1에 가까워짐. 음수일 땐 0에 근접.
- 정분류율 accuracy : 0.77 / 민감도 : 0.91
- 코드 설명
- 1) set.seed(125): 7:3으로 train, test 분할을 하는데 7할의 데이터를 무작위로 뽑기 위해서 난수를 만드는 것이고, 한 번 만든 난수를 고정적으로 활용하기 위해 특정 번호를 부여
※ credit_final.csv 라는 파일은 빅분기 자료실에도 없어 직접 문의하여 수령했습니다.
> credit <- read.csv(file.path(route, "credit_final.csv"))
> class(credit$credit.rating)
[1] "integer"
> # 종속변수 factor 변환
> credit$credit.rating <- factor(credit$credit.rating)
> str(credit)
'data.frame': 1000 obs. of 21 variables:
$ credit.rating : Factor w/ 2 levels "0","1": 2 2 2 2 2 2 2 2 2 2 ...
$ account.balance : int 1 1 2 1 1 1 1 1 3 2 ...
$ credit.duration.months : int 18 9 12 12 12 10 8 6 18 24 ...
$ previous.credit.payment.status: int 3 3 2 3 3 3 3 3 3 2 ...
$ credit.purpose : int 2 4 4 4 4 4 4 4 3 3 ...
$ credit.amount : int 1049 2799 841 2122 2171 2241 3398 1361 1098 3758 ...
$ savings : int 1 1 2 1 1 1 1 1 1 3 ...
$ employment.duration : int 1 2 3 2 2 1 3 1 1 1 ...
$ installment.rate : int 4 2 2 3 4 1 1 2 4 1 ...
$ marital.status : int 1 3 1 3 3 3 3 3 1 1 ...
$ guarantor : int 1 1 1 1 1 1 1 1 1 1 ...
$ residence.duration : int 4 2 4 2 4 3 4 4 4 4 ...
$ current.assets : int 2 1 1 1 2 1 1 1 3 4 ...
$ age : int 21 36 23 39 38 48 39 40 65 23 ...
$ other.credits : int 2 2 2 2 1 2 2 2 2 2 ...
$ apartment.type : int 1 1 1 1 2 1 2 2 2 1 ...
$ bank.credits : int 1 2 1 2 2 2 2 1 2 1 ...
$ occupation : int 3 3 2 2 2 2 2 2 1 1 ...
$ dependents : int 1 2 1 2 1 2 1 2 1 1 ...
$ telephone : int 1 1 1 1 1 1 1 1 1 1 ...
$ foreign.worker : int 1 1 1 2 2 2 2 2 1 1 ...
> # 데이터 분할
> set.seed(125)
> idx <- sample(1:nrow(credit), nrow(credit)*0.7,
+ replace = F)
> train <- credit[idx,]
> test <- credit[-idx,]
> # logistic regression
> log <- glm(credit.rating~.,
+ data = train,
+ family = "binomial")
> summary(log)
Call:
glm(formula = credit.rating ~ ., family = "binomial", data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.4572 -0.8486 0.4517 0.7199 2.3466
Coefficients:
Estimate
(Intercept) -2.9796332
account.balance 0.7899262
credit.duration.months -0.0098140
previous.credit.payment.status 0.5715653
credit.purpose -0.3542261
credit.amount -0.0001622
savings 0.3192383
employment.duration 0.0843606
installment.rate -0.2506252
marital.status 0.1868801
guarantor 0.2402208
residence.duration -0.0486384
current.assets -0.2107500
age 0.0212596
other.credits 0.1231222
apartment.type 0.1506953
bank.credits -0.1686450
occupation 0.0840070
dependents -0.1949538
telephone 0.3241080
foreign.worker 1.1521678
Std. Error
(Intercept) 1.2457188
account.balance 0.1193521
credit.duration.months 0.0100916
previous.credit.payment.status 0.1768527
credit.purpose 0.1024798
credit.amount 0.0000475
savings 0.0923565
employment.duration 0.0976746
installment.rate 0.0971161
marital.status 0.0936263
guarantor 0.3288764
residence.duration 0.0943107
current.assets 0.1092905
age 0.0101630
other.credits 0.2433956
apartment.type 0.2048266
bank.credits 0.2329400
occupation 0.1649549
dependents 0.2744463
telephone 0.2224268
foreign.worker 0.6411033
z value
(Intercept) -2.392
account.balance 6.618
credit.duration.months -0.972
previous.credit.payment.status 3.232
credit.purpose -3.457
credit.amount -3.415
savings 3.457
employment.duration 0.864
installment.rate -2.581
marital.status 1.996
guarantor 0.730
residence.duration -0.516
current.assets -1.928
age 2.092
other.credits 0.506
apartment.type 0.736
bank.credits -0.724
occupation 0.509
dependents -0.710
telephone 1.457
foreign.worker 1.797
Pr(>|z|)
(Intercept) 0.016761 *
account.balance 3.63e-11 ***
credit.duration.months 0.330805
previous.credit.payment.status 0.001230 **
credit.purpose 0.000547 ***
credit.amount 0.000637 ***
savings 0.000547 ***
employment.duration 0.387758
installment.rate 0.009861 **
marital.status 0.045932 *
guarantor 0.465128
residence.duration 0.606046
current.assets 0.053812 .
age 0.036451 *
other.credits 0.612960
apartment.type 0.461900
bank.credits 0.469075
occupation 0.610561
dependents 0.477485
telephone 0.145077
foreign.worker 0.072310 .
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05
‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 858.57 on 699 degrees of freedom
Residual deviance: 679.38 on 679 degrees of freedom
AIC: 721.38
Number of Fisher Scoring iterations: 5
#step function
step.log <- step(glm(credit.rating~1,
data = train,
family = "binomial"),
scope = list(lower = ~1,
upper = ~account.balance +
credit.duration.months +
previous.credit.payment.status +
credit.purpose +
credit.amount +
savings +
employment.duration +
installment.rate +
marital.status +
guarantor +
residence.duration +
current.assets +
age +
other.credits +
apartment.type +
bank.credits +
occupation +
dependents +
telephone +
foreign.worker), direction = "both")
summary(step.log)
> summary(step.log)
Call:
glm(formula = credit.rating ~ account.balance + previous.credit.payment.status +
savings + credit.purpose + current.assets + age + credit.amount +
installment.rate + marital.status + foreign.worker + telephone,
family = "binomial", data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.4197 -0.8314 0.4694 0.7433 2.5162
Coefficients:
Estimate
(Intercept) -2.5852619
account.balance 0.8052006
previous.credit.payment.status 0.5362718
savings 0.3096824
credit.purpose -0.3623654
current.assets -0.2000295
age 0.0232739
credit.amount -0.0001840
installment.rate -0.2520631
marital.status 0.1956085
foreign.worker 1.2003755
telephone 0.3501330
Std. Error
(Intercept) 0.9510327
account.balance 0.1180681
previous.credit.payment.status 0.1550992
savings 0.0906882
credit.purpose 0.1011563
current.assets 0.0985154
age 0.0091675
credit.amount 0.0000372
installment.rate 0.0918919
marital.status 0.0891584
foreign.worker 0.6305047
telephone 0.2106180
z value
(Intercept) -2.718
account.balance 6.820
previous.credit.payment.status 3.458
savings 3.415
credit.purpose -3.582
current.assets -2.030
age 2.539
credit.amount -4.947
installment.rate -2.743
marital.status 2.194
foreign.worker 1.904
telephone 1.662
Pr(>|z|)
(Intercept) 0.006560 **
account.balance 9.12e-12 ***
previous.credit.payment.status 0.000545 ***
savings 0.000638 ***
credit.purpose 0.000341 ***
current.assets 0.042312 *
age 0.011125 *
credit.amount 7.55e-07 ***
installment.rate 0.006087 **
marital.status 0.028240 *
foreign.worker 0.056932 .
telephone 0.096431 .
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05
‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 858.57 on 699 degrees of freedom
Residual deviance: 683.95 on 688 degrees of freedom
AIC: 707.95
Number of Fisher Scoring iterations: 5
> library(caret)
> # 예측값을 response로 지정해 확률값 출력
> pred <- predict(step.log, test[,-1], type = 'response')
> #결과를 dataframe으로 표시
> pre_df <- as.data.frame(pred)
> # 범주 추가
> pre_df$grade <- ifelse(pre_df$pred<0.5,
+ pre_df$grade<-0,
+ pre_df$grade<-1)
> confusionMatrix(data = as.factor(pre_df$grade),
+ reference = test[,1],
+ positive = '1')
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 38 18
1 50 194
Accuracy :
95% CI :
No Information Rate :
P-Value [Acc > NIR] :
Kappa :
Mcnemar's Test P-Value :
Sensitivity :
Specificity :
Pos Pred Value :
Neg Pred Value :
Prevalence :
Detection Rate :
Detection Prevalence :
Balanced Accuracy :
'Positive' Class :
0.7733
(0.7217, 0.8195)
0.7067
0.0057934
0.3882
0.0001704
0.9151
0.4318
0.7951
0.6786
0.7067
0.6467
0.8133
0.6735
1
2. 의사결정나무 Decision Tree
- 의사결정나무 : 분류함수를 의사결정규칙으로 구성된 나무 모양으로 그리는 방법
- 분류나무와 회귀나무 모형이 있음.
- 분석과정 : 성장 - 가지치기 - 타당성 평가 - 해석 및 예측 순
- 1) 성장 : 각 마디에서 적절한 최적 분리규칙을 찾아 나무를 성장시키는 과정. 적절한 정지규칙을 만족하면 멈춤.
- 정지규칙 : 더 이상 분리가 일어나지 않고, 현재 마디가 끝마디 (자식마디가 없는 마디)가 되도록 하는 규칙. 의사결정나무의 깊이를 지정하거나 끝마디 레코드 수의 최소개수를 지정.
- 분리규칙을 설정하는 분리 기준은 이산형, 연속형 목표변수에 따라 나뉨.
- (1) 이산형 목표변수
- 분류나무 : 목표변수가 이산형. 상위 노드에서 가지 분할 시, 분류변수와 분류 기준값의 선택방법으로 카이제곱 통계량의 p값, 지니 지수, 엔트로피 지수 활용.
- (2) 연속형 목표변수
- 회귀나무 : 목표변수가 연속형. 분류변수와 분류 기준값의 선택방법으로 F-통계량 값, 분산의 감소량 등 사용
- 2) 가지치기 : 오차를 크게 할 위험이 높거나 부적절한 추론규칙을 가진 가지를 제거하는 단계
- 나무의 크기 ☞ 모형의 복잡도.
- 마디에 속하는 자료가 일정 개수 이하일 때, 분할을 정지하고 비용-복잡도 가지치기를 활용.
- 3) 타당성 평가 : 이익도표, 위험도표, 시험용 데이터 활용
- 4) 해석 및 예측 단계
- 의사결정나무 알고리즘
- 1) CART (Classification ANd Regression Tree)
- 가장 많이 활용됨. 불순도의 측도로 목적변수가 범주형 - 지니 지수 / 연속형 - 분산을 쓰는 이진분리 활용.
- 이진트리 구조로 모형을 형성하는데 목표변수를 가장 잘 분리하는 설명변수와 그 분리 시점을 찾는 것. 그 척도 중 하나가 다양성이고 다양성을 가장 많이 줄이는 설명변수 선택.
- 2) C4.5 & C5.0
- CART는 이진분리 but C4.5는 각 마디에서 다지분리가 가능.
- training dataset과 멀리 떨어진 데이터에 대하여 언급 X
- 3) CHAID
- 가장 오래됨. SPSS, SAS에 보편적. 두 변수 사이의 통계적 관계를 찾는 것에서 비롯됨.
- 카이제곱 검정 (이산형), F-검정 (연속형)을 활용해 다지분리를 수행하는 알고리즘.
- CART와 달리 오버피팅하기 전, 나무 형성을 멈춤.
- 의사결정나무의 장단점
- 장점 : 직관적. 통계적 가정이 불필요한 비모수적 모형. 수치형, 변수형 모두 취급 가능
- 단점 : 분류 기준의 경계에 있는 자료에 대해 오차 큼. 예측변수의 효과를 파악하기 어려움. 새로운 자료 예측 어려움.
3. 서포트 벡터 머신 SVM
- 패턴 인식, 자료 분석을 위한 지도학습 머신러닝 모델이고 회귀, 분류 문제 해결에 사용됨.
- 주어진 데이터 집합을 토대로 새로운 데이터가 어떤 그룹에 속할 지 판단하는 확률적 이진선형분류모델 생성.
- SVM은 마진 최대화로 일반화 능력의 극대화를 추구하기에 마진이 가장 큰 초평면을 분류기로 사용할 때, 오분류가 가장 적어짐. (↔기존 분류기는 오류 최소화 추구)
- SVM의 원리
- SVM 분류 모델은 데이터가 표현된 공간에서 분류를 위한 경계 정의. (분류되지 않은 값이 들어오면 어느 쪽에 속하는지 판별 시도)
- 결정 초평면 : 데이터의 그룹을 구분하는 분류자. 초평면은 데이터가 존재하는 n차원 보다 한 차원 낮은 n-1차원.
- 서포트 벡터 : 각 그룹의 데이터 중 초평면에 가장 가까운 것. (결정 경계를 지지함)
- 마진 : 서포트 벡터와 초평면 사이의 수직 거리
- 적절한 마진의 선택
- 이상치가 존재할 때, 약간의 오류를 허용하는 파라미터 cost (C) 활용.
- 1) 소프트 마진 : C를 작게 설정해 데이터가 마진 안에 포함되는 것을 허용. 지나치게 많이 허용한다면 Underfitting 문제 발생.
- 2) 하드 마진 : C를 크게 설정. 이상치의 존재를 허용치 않음. Overfitting의 가능성.
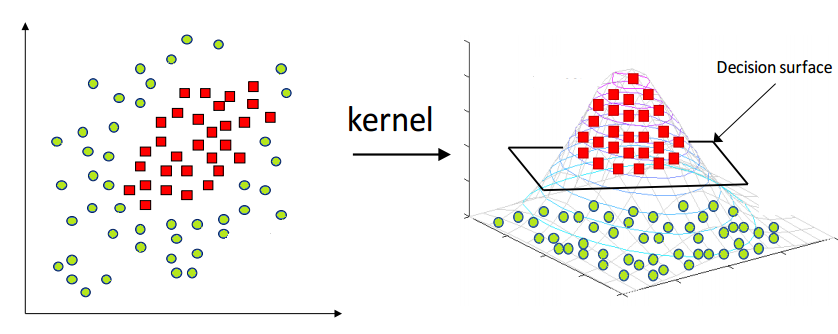
- 커널 Kernel
- SVM 모형은 비선형 분류에서도 사용되는데 입력자료를 다차원 공간으로 매핑하여 해결함. 이 과정에서 커널 함수로 계산량을 줄이는 커널 트릭이 쓰임.
- 커널 트릭의 종류로 선형 커널, 다항식 커널, 시그모이드 커널, 가우시안 RBF 등이 있음. 각 커널마다 최적화를 돕는 매개변수가 있고, 성능은 RBF가 좋은 편.
- SVM의 장단점
- 장점 : 분류, 예측 모두 가능. 신경망에 비해 과적합 정도가 낮음. 저차원, 고차원 데이터에 활용 가능.
- 단점 : 전처리와 매개변수 설정에 따라 정확도 변동. 대용량 데이터 처리 어려움. 예측 원리에 대한 이해 및 해석이 어려움.
4. K-최근접 이웃 알고리즘 K-NN
- 어떤 집단으로 나뉜 데이터셋이 있을 때, 새로운 데이터가 추가되면 무슨 집단으로 분류할 지 결정.
- 지도학습의 한 갈래.
- 원리
- 새 데이터의 범주를 해당 데이터와 가장 가까운 k개 데이터의 범주로 결정.
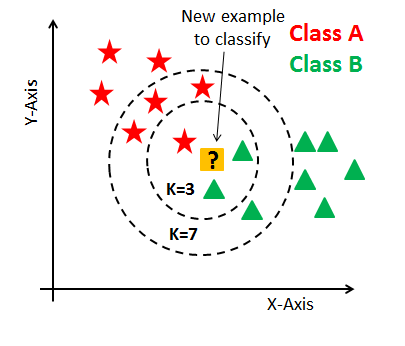
- 이웃 간의 거리 계산
- 유클리디안, 맨하탄, 민코우스키를 슬 수 있고, 유클리디안을 주로 씀.
- K-NN 장단점
- 장점 : 사용법 간단. 범주를 나누는 기준을 몰라도 분류 가능. 추가 데이터 처리 용이
- 단점 : K값 결정 어려움. 수치형이 아닌 데이터의 유사도 정의 어려움. 이상치 영향 큼.
5. 나이브 베이즈 분류
- 나이브 베이즈 분류 : 데이터에서 변수에 대한 조건부 독립을 가정하는 알고리즘. 클래스에 대한 사전정보와 데이터에서 추출한 정보를 결합해 베이즈 정리로 어떤 클래스에 속하는지 분류하는 알고리즘.
- 텍스트 분류에서 문서를 여러 카테고리 중 하나로 분류하는 용도로 사용 가능.
- 베이즈 정리 Bayes theorem
- 두 확률변수의 사전확률과 사후확률의 관계를 표현하는 정리.
- 예) 사건 B가 일어난 것을 전제로 사건 A의 조건부 확률을 구할 수 있음. (A, B 확률 + B조건부 확률 안다는 가정)
- 계산
- 하나의 속성 값을 기준으로 다른 속성이 독립적이라 할 때, 해당 속성 값이 클래스 분류에 끼치는 영향 측정.
- 클래스 조건 독립성 : 속성 값에 대해 다른 속성이 독립적이라는 가정.
6. 앙상블 Ensemble
- 앙상블 : 데이터로 여러 개의 예측모형을 만들고 이를 조합하여 하나의 최종 예측모형을 만드는 기법. 학습방법이 불안전한 의사결정나무에 주로 활용.
- 배깅 bagging : 여러 개의 부트스트랩 자료를 생성하고 각 자료에 예측모형을 만들어 결합.
- 부트스트랩 : 주어진 데이터에서 단순랜덤 복원추출 방법으로 동일한 크기의 표본을 여러 개 생성하는 샘플링 방법.
- 보팅 voting : 여러 개의 모형으로 산출된 결과를 다수결로 선정하는 과정.
- 배깅에서는 가지치기를 하지 않고, 최대로 성장한 의사결정나무 활용.

- 부스팅 boosting : 예측력이 약한 모형을 결합해 강한 예측모형을 만드는 방법. 오분류 데이터에 가중치 부여.
- 훈련오차를 빠르고 쉽게 줄일 수 있고, 배깅에 비해 예측오차가 향상되어 Adaboost의 성능이 배깅보다 좋음
- 1) GBM (Gradient Boosting Machine) : 오차를 미분한 Gradient를 제공해 모델을 보완하는 방식. boosting에서 가중치 업데이트를 경사하강법으로 진행.
- 경사하강법 : 손실함수를 정의하고 이 함수의 미분값이 최소가 되는 방향을 찾아 접근하는 방법.
- 프로세스
- (1) 초기값으로 상수함수 적용
- (2) 손실함수를 최소화하는 Gradient 도출
- (3) Gradient를 베이스 모델의 목표값으로 사용해 학습 진행
- (4) 학습률을 더해 최종모형 생성
- (5) 상기 과정 반복
- 장단점
- 장점 : 랜덤포레스트보다 성능 좋음. 예측 성능 좋음.
- 단점 : 하이퍼 파라미터 튜닝 필요. 과적합 가능성. 대용량 처리 어려움.
- 2) Xgboost : Gradient boosting 알고리즘을 분산환경에서도 실행하게끔 구현. 회귀, 분류 모두 지원. GBM보다 빠르고 오버피팅 방지 규제 포함.
- 3) Light GBM : Xgboost보다 빠르고 대용량 데이터 취급. GPU 지원. but 적은 데이터셋 적용 시, 과적합 가능성.
- 랜덤포레스트
- 의사결정나무의 특징인 분산이 크다는 점을 감안하여 배깅과 부스팅보다 더 많은 무작위성을 부여해 약한 학습기 생성 후, 이를 선형 결합.
- 지도학습 알고리즘. 다수의 의사결정트리 사용. 회귀 - 평균화, 분류 - 투표
- 해석이 어렵지만 예측력이 높음.
- 장점 : 간편&빠름. 다중 클래스 알고리즘. 로버스트. 분류&회귀
- 단점 : 메모리 사용량 많음. 과적합 발생 가능성. 텍스트 데이터 처리 X
- 변수 중요도 : 불순도를 얼마나 감소시키는지로 측정되는 값. (MeanDecreaseAccuracy 등)
2절 연관분석
1. 연관규칙의 개념 및 형태
- 장바구니 분석, 서열 분석 sequence anlaysis 라고도 함.
- 서열 분석 : A를 산 이후 B를 구매한다.
- 조건과 반응의 형태 (if-then)
2. 연관규칙의 측도
산업의 특성별로 지지도, 신뢰도, 향상도를 고려해 규칙을 설정해야 한다.
- 지지도 : A, B가 동시에 포함된 거래수 / 전체 거래수 = P(A∩B)
- 신뢰도 : A, B가 동시에 포함된 거래수 / A가 포함된 거래수 = P(A∩B) / P(A). 연관 정도를 파악할 수 있음.
- 향상도 Lift : A, B가 동시에 포함된 거래수 / A 포함 거래수 x B 포함 거래수 = P(B|A) / P(B) = P(AUB) / P(A)P(B). A가 구매되지 않았을 때, 품목 B의 구매확률에 비해 A가 구매됐을 때, 품목 B 구매확률의 증가비. 서로 관련이 없다면 1이 됨.
- 장단점
- 장점 : 비목적성 분석기법 (목적변수가 없음). 계산 용이
- 단점 : 품목수가 늘어남에 따라 계산 복잡도 증가. 거래량이 적은 품목은 제외됨.
3. Apriori 알고리즘
- 빈발항목집합 : 최소 지지도보다 큰 지지도 값을 갖는 품목의 집합
- Apriori 알고리즘은 모든 품목집합에 대한 지지도를 계산하는 것이 아닌, 최소 지지도 이상의 빈발항목집합을 찾아 이에 대해서만 연관규칙 계산.
- 지지도가 낮은 후보 집합 생성 시, 아이템 개수가 늘어남에 따라 계산이 어려워진다는 단점.
3절 군집분석
1. 개요
- 객체의 유사성을 측정해 유사성이 높은 집단을 분류하고, 군집에 속한 객체의 유사성과 타 군집에 속한 객체의 상이성을 규명하는 분석법.
- 특성에 따라 고객을 여러 배타 집단으로 나눔.
- 군집의 개수나 구조에 대한 가정없이 데이터 간의 거리를 기준으로 군집화 유도. (ex. 마케팅 조사에서 소비자군 분류)
2. 특징
- 요인분석과의 차이 : 요인분석은 유사한 변수를 함께 묶는 것
- 판별분석과의 차이 : 판별분석은 사전에 집단이 나뉜 자료를 통해 새 데이터를 기존 집단에 할당하는 것이 목적.
3. 거리
군집분석에서는 관측 데이터 간 유사성이나 근접성을 측정해 어느 군집으로 묶을지 판단해야 한다.
- 연속형 변수
- 유클리디안 거리 : 데이터 간 유사성 측정. 통계적 개념이 없어 변수의 산포 정도가 고려되지 않음.
- 표준화 거리 : 해당 변수의 표준편차로 척도 변환한후 유클리디안 거리 계산. 표준화로 척도, 분산의 차이로 인한 왜곡 방지
- 마할라노비스 거리 : 변수의 산포를 고려해 표준화한 거리. 두 벡터 사이의 거리를 표본공분산으로 나눔. 그룹에 대한 사전정보 필요.
- 체비셰프 거리 : 두 벡터의 x좌표 차와 y좌표 차 중 큰 값을 갖는 거리
- 맨하탄 거리 : 건물에서 건물로 가기 위한 최단 거리
- 캔버라 거리 : 두 벡터 간의 차에 대한 절대값을 두 벡터의 합으로 나누고 그 값을 모두 더함.
- 민코우스키 거리 : L1 (맨하탄) + L2 (유클리디안)
- 범주형 변수
- 자카드 거리 : 1에서 자카드 계수를 뺀 값.
- 자카드 유사도 : 자카드 계수라고도 함. 두 집합 간의 유사도 측정.0~1 사이로 두 집합이 동일하면 1. J(A, B) = |A∩B| / |AUB| (유사도는 값이 클수록 비슷, 거리는 작을수록 비슷)
- 코사인 거리
- 코사인 유사도
4. 계층적 군집분석
- n개의 군집으로 시작해 군집의 개수를 줄여 나가는 방법.
- 합병형 방법과 분리형 방법이 있음.
- 종류
- 1) 최단연결법 : n*n 거리행렬에서 거리가 가까운 데이터를 묶어서 군집 형성. 최단거리를 거리로 계산해 거리행렬 수정을 진행하고 가까운 데이터를 새로운 군집으로 형성.
- 2) 최장연결법 : 최장거리를 거리로 계산해 거리행렬을 수정.
- 3) 평균연결법 : 평균이 거리의 기준
- 4) 와드연결법 : 편차 제곱합 고려.
- 5) 군집화 : 거리행렬로 가장 가까운 거리에 있는 객체의 관계를 규명하고 덴드로그램을 그림.
- 군집화 단계
- (1) 거리행렬 기준으로 덴드로그램 작성
- (2) 덴드로그램 최상단부터 세로축 개수에 따라 가소선을 그어 군집 개수 선택.
- (3) 객체의 구성을 고려해 적절 군집수 선정
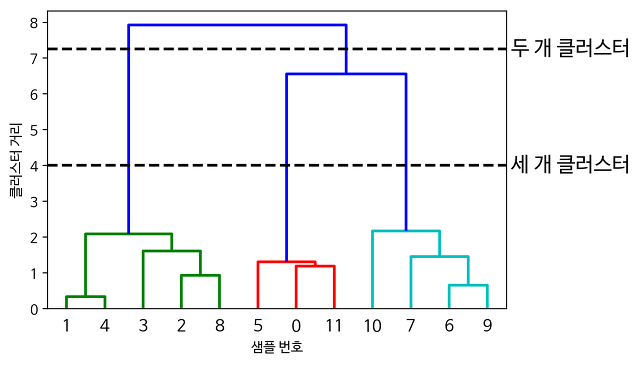
6. 비계층적 군집분석
n개의 개체를 g개의 군집으로 나눌 수 있는 경우의 수를 모두 고려해 최적화한 군집을 형성하는 것.
- K-평균 군집분석 K-means Clustering
- 데이터를 k개의 클러스터로 묶는 알고리즘. 각 클러스터와 거리 차이의 분산을 최소화
- 과정
- 1) 원하는 군집 개수와 초깃값 seed 을 정해 이를 중심으로 군집 형성
- 2) 데이터를 가장 가까운 seed가 있는 군집으로 분류
- 3) 각 군집의 seed 재계산하고 모든 개체가 군집으로 할당될 때까지 상기 과정 반복.
- 최적의 k 찾기
- 1) Elbow 방법 : 군집 수에 따라 군집 내 총제곱합을 플로팅하여 팔꿈치 (비율이 급격하게 작아지는 부분) 의 위치를 적절한 군집 수로 선택하는 방법.
- 2) 실루엣 기법 : 실루엣 계수 (한 클러스터 안에서 데이터가 다른 클러스와 비교해 얼마나 비슷한지 나타낸 것. -1~1) 를 사용한 클러스터링의 품질을 정량적으로 계산하는 방법.
- K-평균 군집분석의 특징
- 1) 연속변수에 활용 가능
- 2) K개의 초기 중심값은 임의로 선택 가능하나 멀리 떨어지는 것이 이상적.
- 3) 탐욕적 알고리즘 : 초기 중심에서 오차제곱합을 최소화하는 방향으로 군집 형성
- 4) 노이즈의 영향이 큼.
- 혼합 분포 군집
- 모형 기반의 군집 방법. 데이터가 k개인 모수적 모형의 가중합으로 표현되는 모집단 모형에서 비롯됐다는 가정 아래, 모수와 가중치를 추정하는 방법을 사용.
- k개의 모형은 군집을 의미.
- 대체로 혼합모형에서 모수와 가중치 추정에 EM 알고리즘 활용됨.
- EM (Expectation-Maximization) 알고리즘 진행 순서
- 1) 데이터에 대해 Z의 조건부분포로부터 조건부 기댓값을 구함.
- 2) 관측변수 X와 잠재변수 Z를 포함하는 로그-가능도 함수에 Z 대신 상수인 Z의 조건부 기댓값 대입하여 로그-가능도 함수를 최대로 하는 모수 도출.
- 특징
- 1) K-평균군집과 유사하나 확률분포를 도입해 군집화 수행
- 2) 군집을 몇 개의 모수료 표현 가능
- 3) 이상치에 민감.
- SOM (Self-Organizing Map)
- 자가조직화지도 SOM 알고리즘은 코호넨 맵이라고도 함.
- 두 개의 인공신경망 층 (입력, 경쟁층)으로 구성.
- 1) 입력층 : 입력변수의 개수와 동일한 뉴런 수. 입력층 자료는 학습을 통해 경쟁층에 정렬되고 이를 지도라 칭함. 입력층의 뉴런은 경쟁층의 뉴런과 연결됨 (fully connected)
- 2) 경쟁층 (2차원 격차로 구성) : 입력벡터의 특성에 따라 벡터가 한 점으로 클러스터링 됨. 승자 독식 구조 - 승자와 유사한 연결 강도를 입력 패턴이 경쟁 뉴런으로 배열
- 특징
- 1) 시각적 이해 용이 (고차원을 저차원으로 표현하기 때문)
- 2) 입력변수의 위치관계를 보존해 실제 데이터가 유사할 경우 지도 상에서 가깝게 표현 (패턴 인식, 이미지 분석에 강점)
- 3) 역전파 알고리즘을 이용하는 인공신경망과 달리 하나의 전방 패스를 사용하므로 속도가 빠름 (실시간 처리)
- 4) 비지도 학습

♧ 예상문제 오답 정리
- 데이터 마이닝 단계 - 데이터 가공 : 모델링 목적에 따라 목적변수를 정리하고 필요한 데이터를 s/w에 적용할 수 있게 준비하는 과정
- 범주 불균형 문제 : 분류 모형을 구성할 때, 예측 실패의 비용이 큰 분류분석의 대상에 대한 관측치가 부족해 모형이 제대로 학습하지 못하는 케이스
- 로지스틱 회귀분석
- 0의 값을 지니는 Y를 정확하게 예측할 때 0에 근접한 매우 작은 cost가 나타남. (1의 값을 가지는 Y를 정확히 예측할 때도 동일)
- 로짓 변환 : y가 -무한대 ~ +무한대가 되도록 변환.
- 의사결정나무 알고리즘
- CART - 이산형 변수 : 지니지수 / 연속형 변수 : 분산감소량
- C5.0 - 이산형 변수 : 엔트로피
- CHAID - 이산형 : 카이제곱 통계랑 / 연속형 : F-통계량
- 의사결정나무 학습방법
- 분리 변수의 P차원 공간에 대한 현재 분할은 이전 분할에 영향을 받는다.
- SVM
- 데이터가 사상된 공간에서 경계로 표현되며, 공간상에 존재하는 여러 경계 중 가장 큰 폭을 지닌 경계를 탐색해 문제 해결
- 신경망에 비해 과적합 정도 낮음.
- 예측 과정과 해석이 쉽지 않음.
- R의 dist 함수가 지원하는 거리 측도 : 유클리디안, 표준화, 캔버라, 민코우스키, 자카드, 맨하탄, 체비셰프, 마할라노비스
- min-max 정규화 : 로데이터 분포를 유지하면서 0~1의 범위로 정규화 가능
- k-means 군집 : 다른 군집으로 이동 가능.
- 앙상블
- 예측치의 분산을 감소시켜 정확도 향상
- 모형의 투명성이 떨어져 원인 분석에는 부적합
- 모형의 상호 연관성이 높을수록 정확도 하락.
- 랜덤포레스트 : 전체 변수 집합에서 부분 변수 집합을 선택해 각 데이터 집합에 대한 모형 생성 후 결합.
- 맨하탄 거리 : |x-y|의 합
- 계층적 군집분석 : 군집의 개수를 미리 지정하지 않아도 되기에 탐색적 분석에 활용.
- 최단연결법은 평균연결법에 비해 계산량이 적다.
- 밀도기반 군집분석 : 반경 내의 최소 개수만큼 데이터 지정 → 임의적인 형태의 군집 탐색에 효과적. DENCLUE, DBSCAN, OPTICS 등.
- 연관분석
- 지나치게 세분화된 경우, 의미가 없어짐.
- 시차 연관분석은 원인과 결과로 해석 가능
- 향상도 계산 (a → b) : p(a∩b) / p(a)p(b)
728x90
반응형
'Cerificate > 빅데이터분석기사' 카테고리의 다른 글
| [빅데이터분석기사 필기] 3과목 - 빅데이터 모델링 (5/5) (0) | 2022.08.17 |
|---|---|
| [빅데이터분석기사 필기] 3과목 - 빅데이터 모델링 (4/5) (0) | 2022.08.17 |
| [빅데이터분석기사 필기] 3과목 - 빅데이터 모델링 (2/5) (0) | 2022.08.11 |
| [빅데이터분석기사 필기] 3과목 - 빅데이터 모델링 (1/5) (0) | 2022.08.10 |
| [빅데이터분석기사 필기] 2과목 - 빅데이터 탐색 (3/3) (어려움) (0) | 2022.08.09 |



