728x90
반응형
지난 포스트에서는 데이터 종류에 따른 EDA에 대해 공부했다. 이번에는 다양한 통계기법을 학습하고자 한다. 이 글은 데이터에듀에서 발행한 '빅데이터 분석기사 필기' 교재의 300~365페이지에 해당하는 내용을 공부한 것이다.
※ 출처가 있는 이미지를 클릭하면 원 사이트로 접속된다.

Index
3장 통계기법의 이해
1) 기술통계
(1) 표본추출
- 용어
- 모집단 : 조사하려는 대상 전체.
- 표본 : 조사하기 위해 뽑은 모집단의 원소.
- 모수 parameter : 표본관측으로 구하려는 정보
- 표집틀 : 표본추출 시 필요한 모집단의 구성 요소와 추출 단계별 표본추출단위가 게재된 목록.
- 표본추출과정 : 모집단 결정 - 표집틀 선정 - 표본추출방법 결정 - 표본크기 결정 - 표본추출
- 표본추출방법 : 확률표본추출 ↔ 비확률표본추출
- 확률표본추출 probability sampling
- 단순랜덤추출법 : N개의 모집단에서 n개의 표본을 무작위로 추출하는 방법
- 계통추출법 : 표본을 k개씩 n개의 구간으로 나누고, 해당 구간의 특정 위치에 있는 원소를 추출하는 것.
- 집락추출법 : 모집단이 복수의 집단으로 구성됐을 떄, 각 집락 cluster 을 랜덤으로 선택해 집락 내에서 임의로 표본을 고르는 것.
- 층화추출법 : 다른 원소로 구성된 모집단에서 각 계층을 대표할 수 있도록 표본을 추출하는 것. 모집단을 겹치치 않는 층으로 나누고, 각 층별로 단순확률표본 추출.
- 비확률 표본추출법 (비무작위표본추출) : 일반화에 제약 있음.
- 편의 표본추출 : 정해진 크기의 표본을 선정할 때까지 조사자 재량껏 원소를 표집하는 방법. (ex - 출구조사)
- 유의 표본추출 (의도적 표본추출) : 조사자의 의도에 따라 대표적인 대상을 표본으로 추출하는 것.
- 지원자 표본추출 (ex - 임상시험)
- 할당 표본추출 : 각 속성의 구성비율을 고려해 표본을 추출하는 것. 선거나 여론조사에서 활용됨.
- 눈덩이 표본추출 (네트워크 표본추출) : 조사 대상자의 소개를 받아 다른 조사 참여자를 구해 조사해나가는 방법.
(2) 데이터 요약
- 자료의 그래프적 표현 : 이산형 자료 - 막대그래프, 원그래프 / 연속형 자료 : 히스토그램, 줄기 잎 그림, 상자그림, 산포도 등
- 자료의 숫자 요약
- 중심 경향도 : 평균, 중앙값, 최빈값
- 산포도 : 분산, 범위, 표준오차, 변동계수
- 비대칭도 : 왜도, 첨도
- 통계량 : 표본으로 얻은 자료의 대푯값. 모수를 추정하는 통계량을 추정량 Estimator 이라고 함.
- 자료의 측정과 형태 : 명목, 순서, 구간, 비율 척도
- 질적 (이산형) 자료 (범주형 자료) : 명목척도 - 어느 집단에 속하는가? (성별, 국적 등), 서열 (순서) 척도 - 일정한 순서. (만족도, 선호도, 학년 등)
- 양적 (연속형) 자료 (수치형 자료) : 구간 (등간) 척도 - 속성의 양 측정. 간격이 유의미. 덧뺄셈 가능. (온도, 지수 등), 비율척도 - 간격에 대한 비율이 유의미. 0 존재. 사칙연산 가능 (무게, 시간, 나이 등)
(3) 확률분포 (교재 참고 요망)
- 확률 Probability은 결과의 가능성을 측정하는 척도. 범위는 0~1.
- 표본공간 Ω의 부분집합인 사건 E의 확률은, 표본공간의 원소 개수에 대한 사건 E의 원소 개수
- 표본공간 : 실험을 반복할 때, 실험으로 거둘 수 있는 모든 결과의 집합
- 확률의 공리 Axioms of Probability
- 확률 계산
- 확률변수 : 정의역 Domain이 표본공간, 치역 Range이 실수값인 함수. (ex. 동전 2개를 던져서 앞면이 나올 경우)
- 이산확률변수 : 이산점에서 0이 아닌 확률값을 가지는 확률변수. (ex. 두 개의 주사위를 던져 나오는 주사위의 합)
- 확률질량함수 : 각 이산점에서 확률의 크기를 표현하는 함수
- 연속형확률변수 : 특정 실수 구간에서 0이 아닌 확률을 갖는 변수. 함수의 형태로 표현.
- 연속형확률변수 X의 확률함수를 f(x)라고 할 때, 이를 확률밀도함수 pdf라고 함.
- 누적 분포 함수 CDF : 특정값 a에 대해 확률변수 X가 X <= a인 모든 경우의 확률의 합을 표현한 것.
- 확률변수의 기댓값(평균)과 분산
- 기댓값 : 확률분포에서 분포의 무게중심. 확률값을 가중치로 하는 일종의 가중평균.
- 두 확률변수의 합의 기댓값은 각 확률변수의 기댓값의 합과 동일.
- 분산 : 확률분포의 산포도를 측정하는 것.
- 확률분포
- 1. 이산형 확률분포
- 베르누이 확률분포 : 결과가 2개만 나오는 경우. 실험의 결과가 성공 or 실패 (상호 배반적 사건)
- 이항분포 : 베르누이 시행을 n번 반복할 때, k번 성공할 확률. 성공 확률 p가 0과 1에 가깝지 않고, n이 충분히 크면 정규분포에 가까워 짐.
- 기하분포 : 성공확률이 p인 베르누이 시행에서 처음 성공이 일어날 때까지 반복한 시행횟수를 X라고 하면, X는 성공확률이 p인 기하분포를 따란다고 함. 기호 X~Geo(p). 단 한 번의 성공을 위해 실패를 거듭해야 하는 경우에 적합.
- 다항분포 : 세가지 이상의 결과가 나오는 반복시행에서의 확률분포 (ex. 주사위 던지기)
- 포아송 분포 : 시간과 공간 내에서 발생하는 사건의 발생횟수에 대한 확률분포.
- 2. 연속형 확률분포
- 균일분포 (일양분포) : 확률변수가 정의되는 구간에서의 확률밀도함수 값이 모두 동일한 확률분포로 정의되는 분포. (ex. 다트)
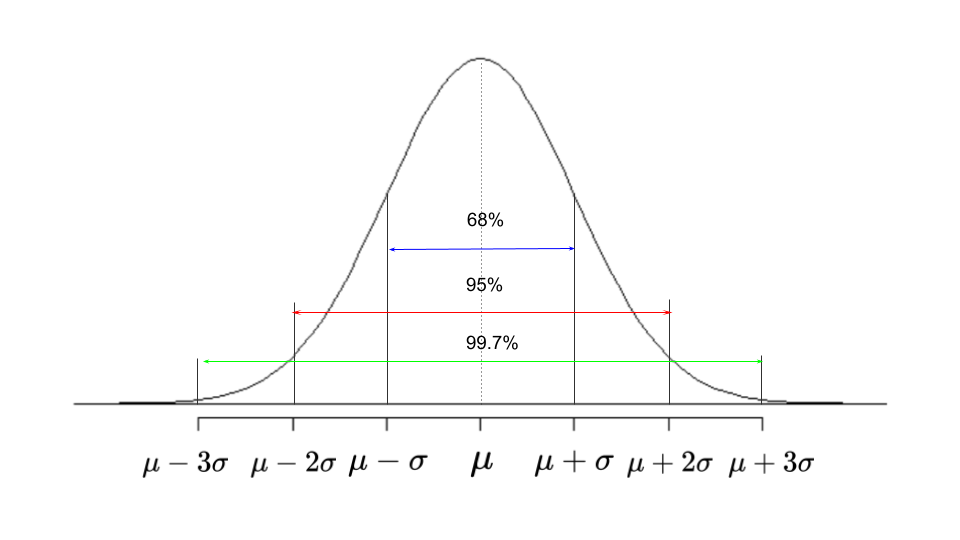
- 정규분포 (가우스 분포) : 평균이 μ (뮤)이고 표준편차가 σ (시그마) 인 x의 확률밀도함수로 종 모양으로 생긴 분포. 정규분포의 모양과 위치는 분포의 평균과 표준편차로 결정됨.
- 표준 정규분포 : 정규분포 중 평균이 0이고, 분산이 1인 정규분포.
- 표준화 : 개별값을 표춘척도로 바꾸는 과정
- 지수분포 : 어떤 사건이 발생할 때까지의 경과시간에 대한 연속확률분포.
- t-분포 : 표준정규분포처럼 평균이 0을 중심으로 좌우가 동일. 확률이 아닌 신뢰구간을 구할 때, 가설검정에서 사용. 표본이 (30개 이상) 커져 자유도가 증가하면 표준정규분포와 동일한 형태가 됨.
- 모표준편차를 모르는 상태에서 표본의 크기가 30보다 작고 집단 간 평균이 동일한지 살펴볼 때 사용.
- 카이제곱 분포 : 모평균과 모분산이 알려지지 않은 모집단의 모분산에 대한 가설검정에서 활용. 두 집간의 동질성 검정 (범주형 자료로 얻은 관측값과 기댓값의 차이를 보는 적합성 검정) 에 활용.
- 분산의 특징을 나타낸 분포. 그래프 상에서는 양의 값만 존재. 오른쪽 꼬리가 긴 비대칭. 자유도가 커지면 모양이 대칭에 근접.
- F-분포 : 두 집단 간 분산의 동일성 검정에 사용되는 분포. 비대칭의 형태. 확률변수는 양의 값만 지니고, 카이제곱 분포와 달리 자유도가 2개.
(4) 표본분포
- 확률표본 : 확률변수 X가 특정 확률분포를 따른다고 할 때, 이 확률분포로부터 독립적으로 관측된 n개의 표본. 이 표본은 서로 독립이고, X와 동일한 분포를 지닌다.
- 확률표본으로 최솟값, 최댓값, 중앙값, 표본평균, 표본분산과 같은 통계량을 정의할 수 있음. 확률변수의 함수로 정의된 통계량도 확률변수임.
- 표본분포 : 한 모집단에서 같은 크기로 뽑을 수 있는 모든 표본에서 통계량을 계산할 때, 이 통계량이 이루는 확률분포.
- 선택된 표본이 포함한 오차의 정도를 측정할 수 있음
- 용어
- 표본오차 : 표본에서 얻은 자료로 모집단의 특성을 추론하여 생기는 오차
- 표준오차 : 통계량의 분포인 표본분포의 표준편차
- 표본평균의 분포 : 모집단에서 같은 크기로 뽑을 수 있는 모든 표본의 평균을 계산할 때, 각 평균이 이루는 확률분포.
- 중심극한정리
2) 추론통계
- 추론통계 : 표본에서 얻은 통계량을 기초로 모집단의 특성 parameter을 추측하는 것.
- 추정 Estimation : 모수가 무엇일지 추측하는 것.
- 가설검정 : 모수에 관한 가설 설정 후, 그 가설의 옳고 그름을 판단해 채택 여부를 정하는 것.
(1) 점 추정
- 확률표본의 정보로 모수에 대한 특정값을 지정하는 것.
- 모평균의 추정량 : 표본평균, 중앙값, 최댓값, 최솟값, 이 둘의 평균.
- 추정량 고려 사항 : 1) 추정량도 특정 확률분포를 지님. 2) 가장 바람직한 추정량 선택
- 불편성 unbiasedness : 추정량의 기댓값은 모수와 편의(차이)가 없음.
- 효율성 : 추정량의 분산이 작을수록 좋음.
- 일치성 : 표본의 크기가 매우 커지면 추정량은 모수와 거의 같아짐.
- 충족성 : 충정량은 모수에 대한 모든 정보를 제공함.
- 모분산의 추정량 : 표본분산은 모분산의 불편추정량 or 최소분산을 가지는 추정량은 아님.
- 모비율의 추정량
(2) 구간추정
- 모수를 특정값으로 지정하는 점추정은 정확성을 판단하기 어려움. 이를 보완하는 것이 구간추정.
- 구간추정 : '확률로 나타낸 신뢰의 정도 하에서 모수가 특정 구간에 있을 것' 이라 선언하는 것.
- 전제 : 1) 추정량의 분포 2) 구해진 구간 내 모수가 있을 가능성의 크기
- 신뢰수준 : 구해진 구간 내 모수가 있을 가능성의 크기. 90, 95, 99%의 확률 주로 사용.
- 신뢰구간 : 각 신뢰수준 하에서 모수가 존재할 것이라고 구한 구간.
- 단일 모수의 신뢰구간 추정
- 1) 모평균의 신뢰구간
- 모평균의 추정량은 표본평균.
- 모평균의 구간추정은 표본평균의 표본분포를 이용하고, 모분산을 아는 경우와 모르는 경우로 구분.
- 2) 모비율의 신뢰구간
- 모비율의 추정량은 표본비율.
- 3) 모분산의 신뢰구간
- 모분산의 추정량은 표본분산.
- 두 모수 차이의 신뢰구간 추정 (서로 독립)
- 1) 두 모평균 차이의 신뢰구간
- 두 모평균 차이의 추정량은 두 표본평균 차이.
- 모평균의 구간추정은 표본평균의 표본분포를 이용하고, 모분산을 아는 경우와 모르는 경우로 구분 (대표본, 소표본).
(3) 최대 우도 추정법
- 모수가 미지의 θ인 확률분포에서 뽑은 표본 x를 바탕으로 θ를 추정하는 기법.
- 우도 likelihood : 주어진 표본 x에 비춰 봤을 때, 모수 θ에 대한 추정이 그럴 듯한 정도.
- 우도 함수 (가능도 함수)
- 확률분포 x에 대한 확률밀도함수 or 확률질량함수 : p(x;θ)
- x : 확률분포를 가질 수 있는 실수, θ : 확률밀도함수의 모수를 의미.
- 확률밀도함수에선 모수 θ가 이미 알고 있는 상수계수, x가 변수.
- 반면, 모수 추정에서는 x를 알고, 모수를 모르기에 반대로 설정.
- 이처럼 확률밀도함수에서 모수를 변수로 보는 경우, 이 함수를 우도 함수라고 한다.
- 표기 : L(θ;x)
- 로그 우도 함수
- 최대 우도 추정법을 활용해 우도가 최대가 되는 θ를 구하려면 수치적 최적화가 요구됨.
- 보통 우도를 직접 사용하는 것이 아니라 로그 변환한 로그-우도 함수를 많이 사용.
- 최대 우도 추정법 : 파라미터로 구성된 어떤 확률밀도함수 p(x|θ)에서 관측된 표본 데이터집합을 x라 할 때, 각 표본에서 파라미터 θ를 추정하는 방법.
- 분포별 최대 우도 추정법
- 베르누이 분포
- 기하 분포
- 포아송 분포
- 정규 분포
- 지수 분포
(4) 가설검정
- 가설설정 : 가설은 모수 (모평균, 모분산, 모비율)에 대해 설정.
- 귀무가설 (H0) : '차이가 없다.', '동일하다'
- 대립가설 (연구가설, H1) : 뚜렷한 증거를 가지고 주장하는 가설. 귀무가설 대신 채택하는 모든 가설.
- 가설검정은 결국, 귀무가설의 채택 여부를 판단하는 과정.
- 검정통계량 T(x) : 가설검정에서 관찰된 표본으로 구하는 통계량 (표본평균, 표본분산, 표본비율). 귀무가설이 옳다고 할 때, 검정통계량 값이 나타날 가능성이 크면 귀무가설 채택.
- 유의수준 α : 귀무가설이 옳음에도 이를 기각하는 확률의 크기. 검정통계량과 무관하게 검정 실시자의 판단에 의거해 결정. 1, 5, 10%를 주로 씀.
- 기각역 C : 검정통계량의 분포에서 확률이 유의수준인 부분.
- 기각역과 유의수준의 관계 : 귀무가설 하에서 검정통계량이 기각역에 속할 확률.
- 유의확률 P-value : 귀무가설의 기각 기준. 검정통계량의 관측결과 값에 따라 귀무가설의 기각이 가능한 최소 유의수준 확률. 귀무가설이 참이라는 가정 하에 얻어진 검정통계량 값에 대응해 구해진 확률.
- 대립가설과 기각역
- 가설검정 단계 : 가설 설정 - 검정통계량과 분포 도출 - 유의수준 결정 및 기각역 설정 - 귀무가설 성립 전제로 표본관찰에 의한 검정통계량 값 도출 - 검정통계량 값이 기각역에 속하면 기각.
- 제1종 오류 α & 제2종 오류 β
- 제1종 오류 : 귀무가설이 옳지만 기각하는 오류. 유의수준과 동일한 확률로 발생.
- 제2종 오류 : 귀무가설이 틀린데도 채택하는 오류
(4) 통계분석 방법론
- 가설의 타당성 여부를 검정하는 방법.
- 단일 모수의 검정
- 1) 모평균의 검정 (t-검정)
- 일표본 t-검정 : 단일 모집단에서 관심있는 연속형 변수의 평균값을 특정 기준값과 비교할 때 사용.
- 종속변수는 연속형 변수.
- 단계 : 가설설정 - 유의수준 설정 - 검정통계량 값 및 유의확률 계산 - 귀무가설 기각 여부 판단 및 의사결정
- 2) 대응표본 t-검정
- 단일 모집단에 두 번의 처리를 가했을 때, 두 번의 처리에 따른 평균의 차이를 비교.
- 예시 : 군인들에게 두 가지 사격 훈련을 실시하고, 적중수 평균에 차이가 있는지?
- 두 모수의 동일성 검정 (독립표본 t-검정)
- 두 개의 독립된 모집단의 평균을 비교.
- 가정 : 정규성, 독립성, 등분산성 (두 독립 집단의 모분산이 동일) 만족. 독립변수는 범주형, 종속변수는 연속형.
- 단계 : 가설설정 - 유의수준 설정 - 등분산 검정 - 검정통계량 값 및 유의확률 계산 - 귀무가설 기각 여부 판단 및 의사결정
3) 분산분석 ANOVA
(1) 일원배치 분산분석 One-way ANOVA
- 분산분석 : 두 개 이상의 집단에서 그룹 평균 간 차이를 그룹 내 변동에 비교하여 살펴보는 방법. 두 개 이상의 집단 평균 차이에 대한 유의성 검증 (평균 비교)
- 일원배치 분산분석 : 반응값에 대한 하나의 범주형 변수의 영향을 알아보기 위해 사용됨. 모집단 수에 제한 없음. F-검정 통계량 사용.
- 가정 : 각 집단의 측정값은 독립적, 정규분포를 따름. 분산 동일.
- 가설 검정 : n개의 집단 간 모평균에 차이가 없다 (귀무)
- 사후 검정 : 귀무가설이 기각돼 평균의 차이가 있다고 할 때, 어떤 집단에서 차이가 있는지 살펴보는 분석. 던컨의 MRt, 피셔의 LSD, 튜키의 HSD 등이 있음.
(2) 이원배치 분산분석
- 분산분석에서 반응값에 대해 두 범주형 변수의 영향을 알아보기 위해 사용되는 방법.
- 예시 : 나이와 성별에 따른 토익점수의 차이.
- 두 독립변수 사이에 상관관계가 있는지 살펴보는 교호작용에 대한 검정이 반드시 요구됨.
- 가정 : 정규분포 (정규성), 등분산성 만족.
- 주효과와 교호작용효과
- 주효과 : 독립변수가 종속변수에 미치는 효과
- 교호작용효과 : 여러 독립변수의 조합이 종속변수에 주는 영향.
- 두 독립변수 사이에 상관관계가 있을 시, 교호작용이 있다는 뜻. 이 경우, 검정이 무의미함.
♤ 참고 자료
- EduAtoZ의 강의와 자료 좋음.
- 유튜브 빅공남 채널의 자료가 유익 - 고등학교 기초 통계, 2과목 통계 재생목록 시청 요망
- 개인 자료 정리 (링크)
♧ 예상문제 오답 정리
- 상자에 포켓몬빵이 50개 있고, 피카츄가 20개, 뮤가 30개 있음. 20개 피카츄 중 3개는 백만볼트를 쓰는 피카츄임. 이 경우, 임의로 포켓몬빵 하나를 뽑을 때 백만볼트 피카츄가 나올 확률은?
- p(백만볼트|피카츄) = 3/50/20/50 = 3/20 = 15%
- A와 B가 독립이라면 ☞ P(A∩B) = P(A) * P(B) / 배반이라면 ☞ P(A∩B) = 0
- 표본편의 Sampiling Bias는 확률화 Randomization로 최소화 및 제거 가능
- 조건부 확률 : 사건 A가 일어났을 때 사건 B가 일어남.
- P(B|A) = P(A∩B)/P(A)
- 두 사건 A, B가 독립이라면, 사건 B의 확률은 A가 일어났다는 가정 하의 B의 조건부확률과 동일. P(B|A) = P(B)
- 연속형 확률밀도함수 : 확률변수 X가 구간 또는 구간들의 모임인 숫자값을 갖는 확률밀도함수.
- 기댓값

- 균일분포의 기댓값 : (a+b) / 2
- 표본의 분산은 카이제곱분포를 따른다.
- 평균 추정의 조건 : 임의성, 일반성, 독립성 ▷ 일반성에 따라 표본평균은 정규분포를 따라야 하나, 모평균은 알 수 없음.
- 99%의 신뢰구간 ▷ 주어진 한 개의 신뢰구간에 모수가 있을 확률이 99%라는 의미.
- X ~ N(10,4)일 때, 6X+6?
- 평균 : 66
- 분산 : 144

- X~N(80,25)일 때, P(60<X<85)?
- 표준화 이후 정규분포표 활용해 계산

- 5지선다형을 5문제를 다 찍을 때, 4문제 맞힐 확률?

- 교차분석 : 두 문항이 모두 범주형일 때 가능.
- 모비율 p의 신뢰구간 구하기...
▣ 문제 및 수정 내역
22.08.09 확률분포, 중심극한정리 공식 및 예제 추가 예정.22.08.10 구간추정 예제 추가 예정.22.09.08 빅공남 정보 추가 (위 2개 내용 해결 가능)
728x90
반응형
'Cerificate > 빅데이터분석기사' 카테고리의 다른 글
| [빅데이터분석기사 필기] 3과목 - 빅데이터 모델링 (2/5) (0) | 2022.08.11 |
|---|---|
| [빅데이터분석기사 필기] 3과목 - 빅데이터 모델링 (1/5) (0) | 2022.08.10 |
| [빅데이터분석기사 필기] 2과목 - 빅데이터 탐색 (2/3) (0) | 2022.08.07 |
| [빅데이터 분석기사 필기] 2과목 - 빅데이터 탐색 (1/3) (0) | 2022.08.05 |
| [빅데이터 분석기사 필기] 1과목 - 빅데이터 분석 기획 (3/3) (0) | 2022.08.04 |