[Practical Statistics for Data Scientists] 3 - 통계적 실험과 유의성 검정

728x90

이전 글 : 2022.08.03 - [데이터/데이터 과학을 위한 통계] - [Practical Statistics for Data Scientists] 2 - 데이터와 표본분포

지난 글에서는 데이터와 표본분포에 대해 공부하였다. 이번 포스트에서는 'Practical Statistics for Data Scientists' 교재의 109~164페이지의 통계적 실험과 유의성 검정에 대한 내용을 다룰 것이다. 코드 또한 필자의 깃허브에서 참조했으니 궁금한 독자들은 본문의 링크를 이용하길 바란다.

<Practical Statistics for Data Scientists> 도서 페이지 : https://bit.ly/3zSetGu

Index

3장 통계적 실험과 유의성 검정

추론 inference : 실험 결과를 더 큰 과정 또는 모집단에 적용하려는 의도 반영
통계 추론 과정 : 가설 수립 - 실험 설계 - 데이터 수집 - 추론 및 결론 도출

1. A/B 검정

A/B 검정 : 두 비교대상 중 한쪽의 우월성을 입증하고자 실험군을 두 그룹으로 나눠 진행하는 실험.
- 대조군 : 두 대상 중 하나는 기존 방법 or 아무 처리도 하지 않는 것.
- 대개 새 방법을 적용한 것이 대조군보다 낫다고 전제
용어 정리
- 처리군 treatment group : 특정 방법이 적용된 집단.
결과를 쉽게 측정할 수 있어 웹 디자인과 마케팅에서 활용됨.

2. 가설 검정 (유의성 검정)

용어 정리
- 귀무가설 : 우연 때문이라는 가설 (유의 : 영가설)
- 대립가설 : 귀무가설과 대조 (증명코자하는 가설)
- 일원검정 : 한 방향으로만 우연히 일어날 확률을 계산하는 가설 검정
귀무가설
- '실제로 우연히 발생했다 해도 그것이 흔하지 않다면 뭔가 의미가 있을 것이라 해석하는 경향이 있다.'는 가정
- 귀무가설이 틀렸다는 것을 입증해 A, B 그룹의 차이가 우연이 아님을 입증하길 원함.
대립가설 : 귀무가설과 대립가설로 모든 가능성을 설명할 수 있어야 함.
일원/이원 가설 검정
- 일원 가설 검정 : 기본값이 지정된 상황에서 유용. (B가 A보다 낫다)
- 이원 가설 검정 : 어느 쪽으로도 속지 않도록. (A는 B와 다르고 크거나 작을 수 있음)
가설검정 : 귀무가설이 사실이라는 전제 하에 영모형 null model을 생성하고 관찰한 효과가 합리적 결과인지 검증하는 것.

3. 재표본추출

재표본추출 : 랜덤한 변동성을 살펴보자는 목표에서 비롯돼, 관찰된 데이터 값에서 표본을 반복적으로 추출하는 것. 몇몇 머신러닝 모델의 정확성 평가 및 향상에 사용됨 (배깅)
부트스트랩 (추정의 신뢰성 평가)과 순열검정이 주요 유형.
용어 정리
- 순열검정 permutation test : 복수의 표본을 결합해 관측값을 무작위로 (혹은 전부로) 재표본으로 추출하는 과정 (유의어 : 임의화검정, 임의순열검정)
- 재표본추출 : 관측 데이터로부터 반복해 표본추출하는 과정
순열검정
- 순서를 바꾸다 permute : 어떤 값들의 집합에서 값들의 순서를 변경한다는 의미
- 절차
  - 1) 여러 그룹의 결과를 단일 데이터 집합으로 합침.
  - 2) 합쳐진 데이터를 섞고, 그룹 A와 같은 크기의 표본을 무작위로 (비복원) 추출
  - 3) 나머지 데이터에서 그룹 B와 같은 크기의 샘플을 무작위로 (비복원) 추출
  - 4) C, D 그룹에 대해서도 동일 작업을 수행하는 것으로 재표본 수집 완료
  - 5) 재표본의 통계량을 계산 및 기록.
  - 6) 상기 단계 R번 반복하여 검정통계량의 순열분포 획득.
- 관찰된 차이가 순열로 보이는 차이의 집합 안에 있다면, 우연히 일어날 수 있는 범위 안에 있다고 해석. 바깥에 있어야 우연이 아닌 것, 즉, 통계적으로 유의미.
R 코드 (pp.121-125)
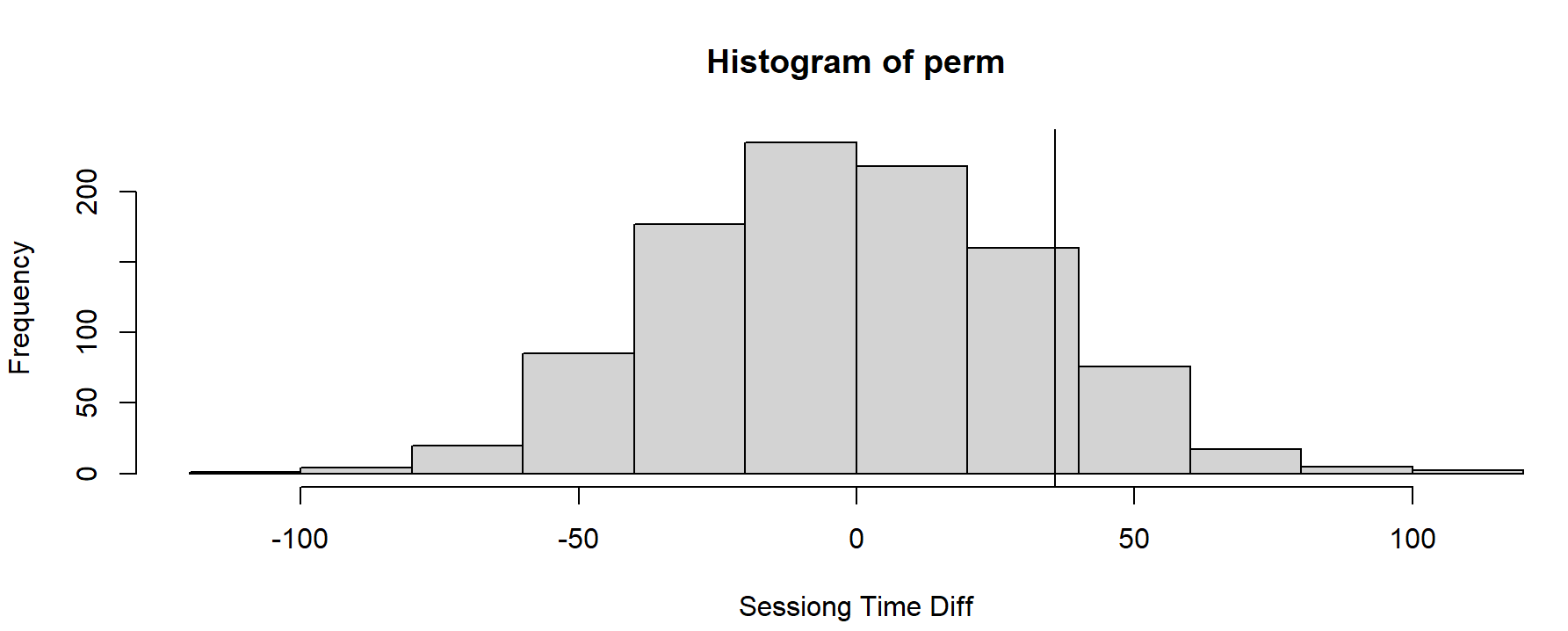
- 페이지 B에서 오랜 시간 머무름.
- 평균 35.67초 더 긺.
- 과연 이 결과가 우연일까? 순열검정으로 확인!
- 수직선은 관측된 차이를 뜻함.

> library(ggplot2)
> setwd('C:/Users/phc07/Desktop/dataHC/01_bigdata/04_PracticalStatistics/Practical_Statistics_DS')
> route <- file.path(getwd())
> session <- read.csv(file.path(route, 'data', 'web_page_data.csv'))
> session[,2] <- session[,2] * 100
> ggplot(session, aes(x = Page, y = Time)) + 
+   geom_boxplot()

> mean_a <- mean(session[session['Page'] == 'Page A', 'Time'])
> mean_b <- mean(session[session['Page'] == 'Page B', 'Time'])
> mean_b - mean_a
[1] 35.66667

> ## Permutation test
> per <- function(x, A, B)
+ {
+   n<- A + B
+   idx_b <- sample(1:n, B)
+   idx_a <- setdiff(1:n, idx_b)
+   mean_diff <- mean(x[idx_b]) - mean(x[idx_a])
+   return(mean_diff)
+ }
> perm <- rep(0,1000) 
> for (i in 1:1000){
+   perm[i] = per(session[,'Time'], 21, 15)
+ }
> hist(perm, xlab = 'Sessiong Time Diff')
> abline(v = mean_b - mean_a)

전체 및 부트스트랩 순열검정
- 상기 랜덤 셔플링 과정을 임의순열검정 random permutation test나 임의화검정 randomization test라고 칭함.
- 이외에 전체순열검정, 부트스트랩 순열검정이라는 유형이 존재.
- 1) 전체순열검정 exhaustive permutation test
  - 데이터를 무작위 셔플&분할해 모든 가능한 조합을 탐색.
  - 샘플이 작을 때 효율적 (모든 조합을 탐색하기 때문)
  - 셔플링을 거듭할수록 임의순열검정의 결과는 전체순열검정의 그것과 근접.
  - 정확검정exact test라고 불림. (영모형보다 정확한 결론을 보장하기 때문.)
- 2) 부트스트랩 순열검정
  - 무작위 순열검정 2, 3단계의 비복원추출을 복원추출로 진행.
  - 개체 선택과 할당의 임의성을 확보.
결론
- 순열검정은 랜덤한 변화가 어떤 영향을 미치는지 파악하고자 사용되는 휴리스틱한 기법. (*휴리스틱 : 직관적인, 어림짐작의) → 해석과 설명이 용이.
- 재표본추출의 장점
  - 1) 숫자형, 이진형 데이터 모두 가능
  - 2) 샘플크기가 달라도 됨.
  - 3) 정규분포가 아니어도 됨.
Point!
- 순열검정으로 복수의 표본을 결합하고 섞은 다음, 섞인 값을 재표본추출하여 표본통계량을 계산. 이 과정을 반복해 재표본추출한 통계를 도표로!
- 관측된 통계량과 재표본추출한 통계라을 비교해 샘플 간의 차이라 우연에서 비롯됐는지 확인할 수 있음.

지금까지 빅데이터분석기사 필기를 준비하고자 R로 진행해왔으나 실기는 python으로 임할 생각이기에 코딩을 python으로 하려고 합니다. 독자 여러분의 양해를 구합니다. (221011)

4. 통계적 유의성과 p값

통계적 유의성 : 본인의 실험 혹은 연구 결과가 우연으로 일어났는지 여부를 판단하는 방법. 우연히 일어날 가능성의 바깥에 속한다면 이를 통계적으로 유의하다고 표현.
키워드
- p 값 p-value : 귀무가설을 구체화한 기회 모델이 주어졌을 때 관측된 값처럼 특이하거나 극단적인 결과를 얻을 확률.
- 알파 : 실제 결과가 통계적으로 의미있다고 여겨지기 위해 우연에 의한 결과가 넘어야 하는 비정상적인 가능성의 임계확률.
- 제1종 오류 : 우연에 의한 효과를 실제 효과로 잘못 판단하는 것
- 제2종 오류 : 실제 효과를 우연으로 잘못 판단하는 것.

결과	A	B
전환	200	182
전환 X	23,539	22,406

A는 B보다 5%가량 우수.
- 200/(23539+200) VS 182/(22406+182)
전환율이 너무 낮아 우연에 의한 차이인지 규명 필요. (귀무가설 : 두 전환율 사이에 차이가 없다.)

※ 코드 참조 : https://bit.ly/3ViSyAN

- for _ in range(1000) 에서 _ 의 의미? 참고

random.seed(1)

obs_pct_diff = 100 * (200 / 23739 - 182 / 22588)
print(f'Observed difference: {obs_pct_diff:.4f}%')

conversion = [0] * 45945
conversion.extend([1] * 382)
conversion = pd.Series(conversion)

perm_diffs = [100 * perm_fun(conversion, 23739, 22588) 
              for _ in range(1000)]

fig, ax = plt.subplots(figsize=(5, 5))
ax.hist(perm_diffs, bins=11, rwidth=0.9)
ax.axvline(x=obs_pct_diff, color='black', lw=2)
ax.text(0.06, 200, 'Observed\ndifference', bbox={'facecolor':'white'})
ax.set_xlabel('Conversion rate (percent)')
ax.set_ylabel('Frequency')

plt.tight_layout()
plt.show()

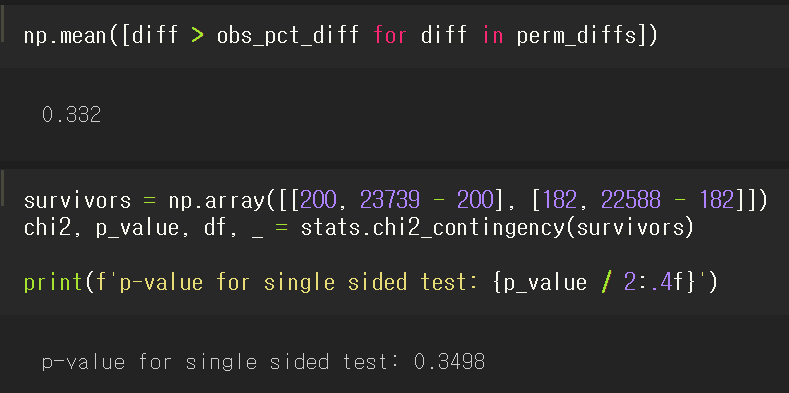
p 값
- 순열검정으로 0.332, 정규근사법으로 0.3498이라는 p 값 확인.
- 가설이 이항분포를 따르므로 p 값 근사 가능.

유의수준
- 무작위 모델이 주어졌을 때 극단적 결과가 나올 확률은 어느 정도인가? → 랜덤 모델의 적합도를 역추적.
- 많은 연구자들이 p 값이 무엇인지도 모르면서 논문이 통과되도록 유의미한 값이 나올 때까지 가설검정 반복. (신랄하다...)
- p값으로 전달코자 하는 것 : 결과가 우연에서 비롯될 확률
- 실제 p값 : 무작위 모델이 주어졌을 때 극단적 결과가 나올 확률
- 2016년 3월, 미국통계협회의 성명서
  - 1) p값은 이 데이터가 특정 통계 모델과 얼마나 상반되는지 나타낼 수 있음.
  - 2) p값은 연구가설이 참일 확률 혹은 데이터가 랜덤하게 생성되었을 확률을 측정하는 것이 아님.
  - 3) 과학적 결론, 비즈니스, 정책 결정은 p값이 특정 임곗값을 통과하는 여부를 기준으로 정해서는 안됨.
  - 4) 적절한 추론을 위해 완전한 보고와 투명성이 요구됨.
  - 5) p값 혹은 통계적 유의성은 효과의 크기나 결과의 중요성을 뜻하지 아니함.
  - 6) p값 그 자체는 모델 또는 가설에 대한 증거를 측정하기 위한 좋은 지표가 아님.
1종 오류 & 2종 오류
- 유의성검정(가설검정)의 기본 기능은 우연에 현혹되지 않도록 하는 것. → 1종 오류를 최소화하도록 가설 설계.
- 2종 오류는 오류라기보다 표본크기가 너무 작아 효과를 알 수 없음을 의미. p값이 통계적 유의성에 미치지 못하는 경우 (ex. 5% 초과), 효과가 아직 입증되지 않음을 뜻함. → 표본이 커질수록 p값 감소.
Point!
- 유의성검정은 관찰값이 귀무가설 모형에 대한 랜덤 변이의 범위 안에 있는지 판단하는 데 사용.
- p값 : 귀무가설에서 비롯된 결과가 관찰된 결과만큼 극단적으로 나올 확률.
- 유의수준 (알파) : 귀무가설 모델에서 '비정상'이라 판단할 임곗값.

5. t 검정

윌리엄 고셋이 단일 표본평균의 분포를 근사하고자 만듦,
키워드
- 검정통계량 test statistic : 관심의 차이 또는 효과에 대한 측정 지표
- t 통계량 : 평균처럼 표준화된 형태의 일반적 검정통계량
- t 분포 : 관측된 t 통계량을 비교할 수 있는 기준분포
python의 scipy.stats.ttest_ind 함수로 t-test 가능
- 대립가설 : 페이지 A의 평균 세션 시간이 페이지 B의 평균보다 작음.

ttest = stats.ttest_ind(session_times[session_times.Page == 'Page A'].Time, 
                      session_times[session_times.Page == 'Page B'].Time,
                      equal_var=False)
print(f'p-value for single sided test: {ttest.pvalue / 2:.4f}')

6. 다중검정

데이터를 충분히 괴롭히다 보면 언젠가 뭐든 털어놓을 것이 있다.

20개의 예측변수와 1개의 결과변수를 무작위 생성
유의수준 0.05로 20번의 유의성검정을 실시하면 적어도 하나의 예측변수에서 통계적으로 유의미한 결과를 초래. (실수)☞ 1종 오류
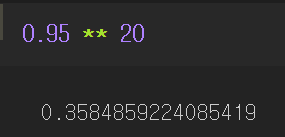
유의미한 결과가 아닐 확률 : 1 - 0.05 = 0.95
20번 모두 무의미한 결과가 나올 확률 : 0.95^20 = 0.36 이므로 최소 한 번은 유의미할 확률이 0.64 ☞ 알파 인플레이션

알파 인플레이션은 데이터마이닝에서 오버피팅 (모델이 노이즈까지 학습)을 야기할 수 있음.
추가되는 변수와 모델이 많을수록 우연으로 유의미하다고 판단할 확률도 높아짐.
- 따라서 지도학습에서는 홀드아웃 세트를 사용.
키워드!
- 1종 오류 : 어떤 결과가 통계적으로 유의미하다고 잘못 판단할 확률.
- 거짓발견비율 FDR : 다중검정에서 1종 오류가 발생하는 비율
- 알파 인플레이션 : 1종 오류를 만들 확률인 알파가 많은 테스트를 거듭할수록 증가하는 다중검정 현상.
- p 값 조정 : 동일한 데이터로 다중검정을 수행하는 경우에 필요
통계학의 수정 : 단일 가설검정보다 통계적 유의성에 대한 기준을 엄격하게!
- 일반적으로 검정횟수에 따라 유의수준을 나눔.
- 본페로니 수정 Bonferroni adjustment : 알파를 비교 횟수 n으로 나눔.
- 투키의 정직유의차 HSD : 복수 집단의 평균을 비교할 때 쓰임.

7. 자유도

표본 데이터로 계산된 통계량에 적용되고 변화가 가능한 값들의 개수를 표현. (ex.10개의 값으로 이뤄진 표본에서 평균을 안다고 가정했을 때, 9개의 자유도가 존재. → 10번째는 계산 가능하고, 자유롭게 변경할 수 없음.)
자유도 모수는 분포의 모양에 영향을 미침.
데이터 과학의 유의성 검정 측면에서는 자유도가 중요치는 않음. but 회귀에서 요인변수를 사용할 땐 중요.
- 범주형 변수를 더미변수화할 때, 빈번.
- 일주일은 7일인데 요일을 지정 시, 자유도는 6개.
- 모든 요일을 포함하면 다중공선성 오차로 회귀 실패.
Point!
- 자유도는 검정통계량을 표준화하는 계산의 일부로, 이로써 기준분포(t분포, F분포 등)와 비교 가능
- 회귀 시, 범주형 변수를 n-1 지표 혹은 더미변수로 요인화하는 이유.

8. 분산분석

ANOVA : 여러 그룹 간에 통계적으로 유의미한 차이를 검정하는 통계적 절차
Keywords!
- 쌍별 비교 pairwise comparison : 여러 집단 중 두 집단 간의 가설검정
- 총괄검정 omnibus test : 여러 그룹 평균들의 전체 분산에 대한 단일 가설검정
- 분산분해 : 구성 요소의 분리. (ex - 전체 평균, 잔차 오차 등으로부터 개별값에 대한 기여)
- F 통계량 : 그룹 평균 간 차이가 랜덤 모델로 예상되는 것으로부터 이탈하는 정도를 나타내는 표준화된 통계량
- SS : 특정 평균으로부터의 편차 제곱합
4개의 웹페이지 비교
- 각각은 꽤 상이한 차이를 보임
- 한 쌍씩 비교하면 횟수가 증가할수록 우연에 속을 가능성이 높아짐.
- ☞ 모든 페이지가 동일한 점착성을 지니는지? 이들의 차이는 우연이고, 페이지 할당 세션 시간 역시 랜덤? 과 같은 질문을 다루는 전체적인 총괄검정을 실시

four_sessions = pd.read_csv(FOUR_SESSIONS_CSV)

ax = four_sessions.boxplot(by='Page', column='Time', figsize=(4, 4))
ax.set_xlabel('Page')
ax.set_ylabel('Time (in seconds)')
plt.suptitle('')
plt.title('')
plt.tight_layout()
plt.show()

순열검정
- 재표본추출한 분산이 고나찰된 변화를 초과한 시간 → p-value
- p-value가 0.07이라면, 7%의 확률로 실제 관측된 값과 다른 경우가 우연히 발생 (임곗값인 5%보다 크므로 귀무가설을 채택함.)
- python은 R과 달리 순열검정을 지원하는 함수가 없어 직접 코딩해야되나?

observed_variance = four_sessions.groupby('Page').mean().var()[0]
print('관측 평균값:', four_sessions.groupby('Page').mean().values.ravel())
print('분산:', round(observed_variance, 3))

# 순열검정
def perm_test(df):
    df = df.copy()
    df['Time'] = np.random.permutation(df['Time'].values)
    return df.groupby('Page').mean().var()[0]
    
print(perm_test(four_sessions))

F 통계량
- 두 집단의 평균비교를 위해 순열검정 대신 t 검정을 쓸 수 있는 것처럼, F 통계량을 사용하는 ANOVA 통계검정도 존재.
- F 통계량은 잔차 오차로 인한 분산과 그룹 평균 (처리 효과)의 분산에 대한 비율에 기반.→ 비율이 높을수록 유의미.
- 데이터가 정규성을 띠면, 해당 통계량은 특정 분포를 따름.
- 다행히 python에서도 statsmodel 패키지로 ANOVA 구현 가능.
- sum_sq : 제곱합, mean_sq : 평균제곱편차
- F통계량 = MS (처리) / MS (오차)

model = smf.ols('Time ~ Page', data=four_sessions).fit()
                
anv_table = sm.stats.anova_lm(model)
print(anv_table)

이원 분산분석
- 위에서는 Page라는 요소에 대해서만 분석
- 이번에는 주말과 평일이라는 두 요소를 분석한다고 가정.
- 총평균 효과와 처리효과를 확인하고, 각 집단의 주말과 평일 데이터를 분리. 그 후, 부분집합의 평균과 처리 평균 사이의 차이를 탐색.
Points!
- ANOVA : 여러 그룹의 실험결과 분석을 위한 통계적 절차
- A/B test와 유사한 절차를 확장해 그룹 간 전체 편차가 우연히 생기는 범위 내에 있는지 평가하고자 사용
- 그룹 처리, 상호작용 효과, 오차에 관한 분산의 구성요소 구분에서 강점을 드러냄.

9. 카이제곱 검정

횟수 관련 데이터에 주로 사용. 예상 분포와 얼마나 적합한지 검정.
관습적으로 변수의 독립성에 대한 귀무가설의 타당성 평가를 위해 r x c 분할표 (r = row, c = column) 함께 사용.
칼 피어슨이 1900년에 개발.
Keywords!
- 카이제곱 통계량 : 기댓값으로부터 어떤 관찰값까지의 거리를 나타내는 측정치
- 기댓값 : 특정 가정 (대개 귀무가설)으로 데이터가 발생할 때, 이에 대한 기대 정도
재표본추출방법
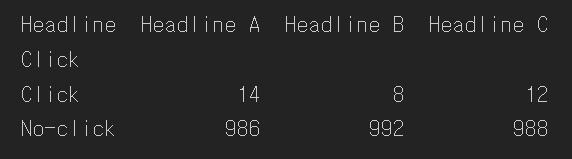
- 클릭률이 우연히 발생할 수 있는 것보다 유의미하게 높은지 검정
- 클릭의 기대 분포 필요
- 귀무가설 : 각 헤드라인이 모두 동일한 클릭률을 가짐.
- 피어슨 잔차 : R = 관측값 - 기대값 / 기댓값의 제곱근
- 순열검정 코드는 과정을 이해하지 못한 자는 쓰지 못할 듯하다 ㅠㅠ

# Resampling approach
box = [1] * 34
box.extend([0] * 2966)
random.shuffle(box)

def chi2(observed, expected):
    pearson_residuals = []
    for row, expect in zip(observed, expected):
        pearson_residuals.append([(observe - expect) ** 2 / expect
                                  for observe in row])
    # return sum of squares
    return np.sum(pearson_residuals)

expected_clicks = 34 / 3
expected_noclicks = 1000 - expected_clicks
expected = [34 / 3, 1000 - 34 / 3]
chi2observed = chi2(clicks.values, expected)

def perm_fun(box):
    sample_clicks = [sum(random.sample(box, 1000)),
                     sum(random.sample(box, 1000)),
                     sum(random.sample(box, 1000))]
    sample_noclicks = [1000 - n for n in sample_clicks]
    return chi2([sample_clicks, sample_noclicks], expected)

perm_chi2 = [perm_fun(box) for _ in range(2000)]

resampled_p_value = sum(perm_chi2 > chi2observed) / len(perm_chi2)
print(f'Observed chi2: {chi2observed:.4f}')
print(f'Resampled p-value: {resampled_p_value:.4f}')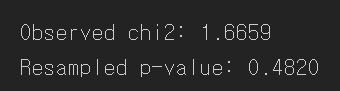

카이제곱 검정 : 통계적 이론
- 점근적 asymptotic 통계 이론은 카이제곱 통계량의 분포가 카이제곱분포로 근사화될 수 있음을 나타냄.
- 적절한 표준 카이제곱분포는 자유도로 결정 → d.f = (r-1)(c-1)
- 보통 오른쪽으로 긴꼬리를 가지고, 관찰 통계량이 분포의 바깥에 있을수록 p-value 작다.
- 하지만, 통계에 약한 데이터 분석가들을 위해 python과 R은 엄청난 혜택을 준다..!
- p-value가 재표본추출로 얻은 것보다 작은데 이는 근사치이기 때문.

chisq, pvalue, df, expected = stats.chi2_contingency(clicks)
print(f'Observed chi2: {chisq:.4f}')
print(f'p-value: {pvalue:.4f}')

피셔의 정확검정
- 카이제곱분포는 재표본검정의 좋은 근사치 제공 (빈도가 낮은 경우 (5개 이하) 제외)
- 예외적인 경우에도 재표본추출로 정확한 p 값 확보 가능
- python은 쉽게 구현할 방법 없음.
데이터 과학과의 연관성
- 카이제곱 검정, 피셔의 정확검정은 어떤 효과가 실제인지 우연인지 확인하고자 사용.
- 고전적 통계 응용 분야에서 카이제곱검정은 통계적 유의성을 결정하는 역할이고, 연구 혹은 실험이 논문에 올라가기 전 수행해야 함. ↔ 데이터 과학에서는 통계적 유의성이 아닌 최적의 처리 방법을 찾는 것이 목표라 멀티암드 밴딧이 더 적합.

10. 멀티암드 밴딧 알고리즘

전통적 통계 방식보다 명시적인 최적화와 보다 빠른 의사결정이 가능하고, 주로 웹테스트에서 활용.
Keywords!
- 멀티암드 밴딧 MAB : 손잡이가 여러 개인 가상의 슬롯머신. 각 손잡이는 제각기 다른 보상을 줌. 다중처리 실험에 대한 비유라고 보면 됨.
- 손잡이 : 실험에서 특정 하나의 처리
가장 높은 승률의 선택지를 취하나 다른 선택지도 테스트하여 최대의 수익을 거두고자 함.
잡아당기는 비율을 수정하는 알고리즘
- 엡실론-그리디 알고리즘
  - 1) 0~1 사이의 균등분포의 난수 생성
  - 2) 난수가 0과 엡실론 (0과 1사이의 값) 사이에 있으면 50대50 확률로 동전 뒤집기 실시 (앞면 - A, 뒷면 - B)
  - 3) 숫자가 엡실론보다 크다면 가장 좋은 보상을 취한 선택지를 취함.
  - 엡실론이 0 → 탐욕 알고리즘, 즉 최상의 즉각적 옵션 (지역 최적) 선택.
- 톰슨의 샘플링
  - 베이즈 방식 사용
  - 베타 분포로 수익의 일부 사전분포 가정
3가지 이상의 처리를 효율ㅈㄱ으로 다루고 최고를 위한 최적의 선택의 하도록 도움.

11. 검정력과 표본크기

Keywords!
- 효과크기 : 통계검정으로 판단할 수 있는 효과의 최소 크기
- 검정력 : 주어진 표본크기로 효과크기를 알아낼 확률
- 유의수준 : 검증 시 사용할 통계 유의 수준
- ex) 20타석에서 3할 타자와 2할타자를 구분할 확률 0.75라 가정.
  - 효과크기 : 1할
  - n = 20
  - 75%의 검정력
표본크기
- 검정력 계산의 주목적 : 표본크기의 필요량 추정.
- 표본크기, 알아내고자 하는 효과크기, 유의수준, 검정력 중 3개를 정하면 나머지 하나 추정 가능.

effect_size = sm.stats.proportion_effectsize(0.0121, 0.011) # 효과크기 계산
analysis = sm.stats.TTestIndPower() # 표본크기 계산
result = analysis.solve_power(effect_size=effect_size, 
                              alpha=0.05, power=0.8, alternative='larger')
print('표본크기: %.3f' % result)

Points!
- 통계검정을 진행하기 전, 포뵨크기의 필요량을 미리 고려해야 함.
- 확인하고자 하는 효과의 최소크기, 검정력 (효과크기를 알아내기 위해 요구되는 확률), 유의수준을 지정해야 함.

상당히 어렵다... 앞으로 계속할지, 기초 개념을 다지고 진행할지 고민된다.

이 챕터의 핵심은 기존의 통계 체계에서 번거로웠 것이 데이터 과학에서는 쉽게 분석할 수 있도록 대체되었거나 필요가 없어졌다는 것이 아닐까. 그럼에도 랜덤 변이가 사람을 혼란스럽게 한다는 사실을 이해하는 것만은 중요하다고 맺음말로 강조하고 있으니 유념하자.

728x90

저작자표시 비영리 변경금지

'Statistics > 데이터 과학을 위한 통계' 카테고리의 다른 글

[Practical Statistics for Data Scientists] 2 - 데이터와 표본분포 (0)	2022.08.03
[Practical Statistics for Data Scientists] 1 - 탐색적 데이터 분석 (EDA) (0)	2022.08.02

From I to T

[Practical Statistics for Data Scientists] 3 - 통계적 실험과 유의성 검정

3장 통계적 실험과 유의성 검정

1. A/B 검정

2. 가설 검정 (유의성 검정)

3. 재표본추출

4. 통계적 유의성과 p값

5. t 검정

6. 다중검정

7. 자유도

8. 분산분석

9. 카이제곱 검정

10. 멀티암드 밴딧 알고리즘

11. 검정력과 표본크기

'Statistics > 데이터 과학을 위한 통계' 카테고리의 다른 글

티스토리툴바

[Practical Statistics for Data Scientists] 3 - 통계적 실험과 유의성 검정

3장 통계적 실험과 유의성 검정

1. A/B 검정

2. 가설 검정 (유의성 검정)

3. 재표본추출

4. 통계적 유의성과 p값

5. t 검정

6. 다중검정

7. 자유도

8. 분산분석

9. 카이제곱 검정

10. 멀티암드 밴딧 알고리즘

11. 검정력과 표본크기

'Statistics > 데이터 과학을 위한 통계' 카테고리의 다른 글

'Statistics/데이터 과학을 위한 통계' Related Articles

티스토리툴바