728x90
반응형
빅데이터 분석기사 필기를 준비하는 데 도움이 되고자 R로 'Practical Statistics for Data Scientists' 교재의 공부를 시작한다. 이 책은 우리말로는 '데이터 과학을 위한 통계'로 번역됐다. 코딩은 RStudio 22.07.1 버전으로 진행할 것이다. 교재에는 파이썬과 R 코드가 모두 적혀있기 때문에 어느 쪽을 써도 무방하다. 다만, 코드가 생략된 부분이 있기 때문에 완전한 코드를 확인하려면 저자의 깃허브를 확인하는 것이 좋다. 이번 포스트에서는 19~66페이지의 탐색적 데이터 분석에 대한 내용을 배울 것이다.

<Practical Statistics for Data Scientists> 도서 페이지 : https://bit.ly/3zSetGu

- 존 투키의 1977년 저서로 EDA가 정립됨.
- 요약통계량 (평균, 중앙값, 분위수 등) + 도표 (상자그림 등) 제시
1. 정형 데이터의 종류 : S/W에서 데이터를 종류별로 구분.
- 수치형 데이터 : 숫자로 나타낸 데이터
- 연속형 데이터 : 일정 범위에서 어떤 값이든 가질 수 있는 데이터 (구간형, 실수형 데이터 - ex. 풍속, 지속 시간)
- 이산 데이터 : 정수만 취할 수 있는 데이터 (정수형 데이터 - ex) 교통사고 발생 횟수)
- 범주형 데이터 : 가능한 카테고리 내의 값을 취하는 데이터 (목록, 명목, 다항형 데이터)
- 이진 데이터 : 값이 2개인 데이터 (참/거짓, 남/여, 0/1)
- 순서형 데이터 : 수치 사이에 순위가 있는 데이터 (성적, 평점 등)
2. 테이블 데이터
- 피처 : 테이블의 열 (속성, 특징, 예측변수)
- 레코드 : 테이블의 행 (관측값, 샘플, 케이스)
3. 위치 추정
- 데이터를 살펴보는 가장 기초적인 단계는 변수의 '대표값'을 구하는 것
- 평균 : 모든 값의 총합을 전체 개수로 나눈 값
- 절사평균 : 크기 순으로 정렬된 데이터를 양끝에서 일정 개수만큼 제거하고 구한 평균. (극단값 영향 최소화)
- 가중평균 : 각 데이터에 가중치를 곱한 후, 그 값의 총합을 가중치의 총합으로 나눈 것.
- 중간값 : 데이터를 정렬했을 때, 정중앙에 있는 값.
- 샘플 코드 (미국 인구)
- 양끝에서 15%를 제외한 절사평균을 구함.
- 가중 평균과 가중 중간값을 구하는 것도 가능.
> USA <- read.csv('./data/state.csv')
> mean(USA[['Population']])
[1] 6162876
> mean(USA[['Population']], trim = 0.15)
[1] 4589490
> median((USA[['Population']]))
[1] 4436370> library('matrixStats')
> weighted.mean(USA[['Murder.Rate']], w = USA[['Population']])
[1] 4.445834
> weightedMedian(USA[['Murder.Rate']], w = USA[['Population']])
[1] 4.44. 변이 추정 : 데이터 밀집 or 분포 ==> 산포도를 표현.
- 편차 (deviation) : 관측값과 위치 추정값의 차 (오차, 잔차)
- 평균을 기준으로 편차의 합은 항상 0
- 평균절대편차 : 편차의 절대값의 평균
- 분산 : 평균과의 편차를 제곱한 값들의 총합을 n-1로 나눈 것 (평균제곱 오차, 제곱편차의 평균)
- 표준편차 : 분산의 제곱근 (루트 분산), 분산보다 해석이 쉬움.
- n-1로 나눠야 비편향 추정.
- 분산, 표준편차는 제곱한 값을 쓰기 때문에 이상치에 민감.
- 중위절대편차 (MAD) : 중간값과의 편차를 구하고, 그 값들의 절대값에 대한 중간값.

- 순서통계량 : 정렬된 데이터를 표현하는 통계량
- 백분위수 = 분위수 (0.3분위수 = 30번째 백분위수)
- 중간값 = 50번째 백분위수
- 사분위범위 (IQR) : 25, 75번째 백분위수의 차
> sd(USA[['Population']])
[1] 6848235
> IQR(USA[['Population']])
[1] 4847308
> mad(USA[['Population']])
[1] 38498705. 데이터 분포 탐색
- 백분위수 : 분포의 꼬리 부분 (외측 범위)를 표현하기 좋음. (ex.상위 99번째 백분위수 = 상위 1%)
- 상자그림 : 백분위수를 활용한 데이터 분산의 시각화 방법.
quantile(USA[['Murder.Rate']], p= c(.05, .25, .5, .75, .95))
5% 25% 50% 75% 95%
1.600 2.425 4.000 5.550 6.510
> boxplot(USA[['Population']] / 1000000, ylab = '인구' )
- 도수분포표와 히스토그램
range <- seq(from = min(USA[['Population']]),
+ to = max(USA[['Population']]),
+ length = 11)
> pop <- cut(USA[['Population']], breaks = range,
+ # right : 구간의 오른쪽값 포함 여부
+ right = T,
+ # 가장 작은 값이 breaks 포인터와 같을 때, 포함 여부
+ include.lowest = T)
> table(pop)
pop
[5.64e+05,4.23e+06] (4.23e+06,7.9e+06] (7.9e+06,1.16e+07]
24 14 6
(1.16e+07,1.52e+07] (1.52e+07,1.89e+07] (1.89e+07,2.26e+07]
2 1 1
(2.26e+07,2.62e+07] (2.62e+07,2.99e+07] (2.99e+07,3.36e+07]
1 0 0
(3.36e+07,3.73e+07]
1
> hist(USA[['Population']], breaks = range)

- 밀도그림 : 부드러운 히스토그램. 데이터 분포를 곡선으로 보여줌.
- freq의 기본값은 Null이고, 이 경우 빈도를 나타냄.
- False로 하면, 밀도를 나타내고 막대의 합은 1이 됨.
hist(USA[['Murder.Rate']], freq = F)
lines(density(USA[['Murder.Rate']]), lwd= 3, col ='skyblue')
6. 이진 데이터와 범주 데이터 탐색
- 범주형 데이터는 주로 비율로 탐색.
- 공항 딜레이 사유
- 국내편 (Inbound) 지연으로 인한 국외편 항공기가 연착되는 것일까?
> # airport delay
> airport <- read.csv('./data/dfw_airline.csv')
> barplot(as.matrix(airport) / 6, cex.axis = 0.6, cex.names = 0.5,
+ xlab = 'Reason of delay', ylab = 'count')
- 막대 그래프와 히스토그램의 차이
- 막대그래프의 X축은 다른 범주지만 히스토그램은 하나의 변수
- 히스토그램의 막대는 밀착됨.
- 기댓값 : 발생할 확률을 가중치로 하는 가중평균
7. 상관관계
- 상관계수 : 숫자형 변수들 사이에 어떤 관계가 있는지 나타내는 측정량 (-1~1)
- 상관행렬
- corrplot 설치부터 진행해야 함.
- 2012년 7월 1일 이후, 섹터가 etf인 심볼 컬럼에 있는 데이터
install.packages("corrplot")
library(corrplot)
sp <- read.csv('./data/sp500_data.csv')
sp_s <- read.csv('./data/sp500_sectors.csv')
etf <- sp[row.names(sp) > "2012-07-01",
sp_s[sp_s$sector == 'etf','symbol']]
corrplot(cor(etf), method = 'ellipse')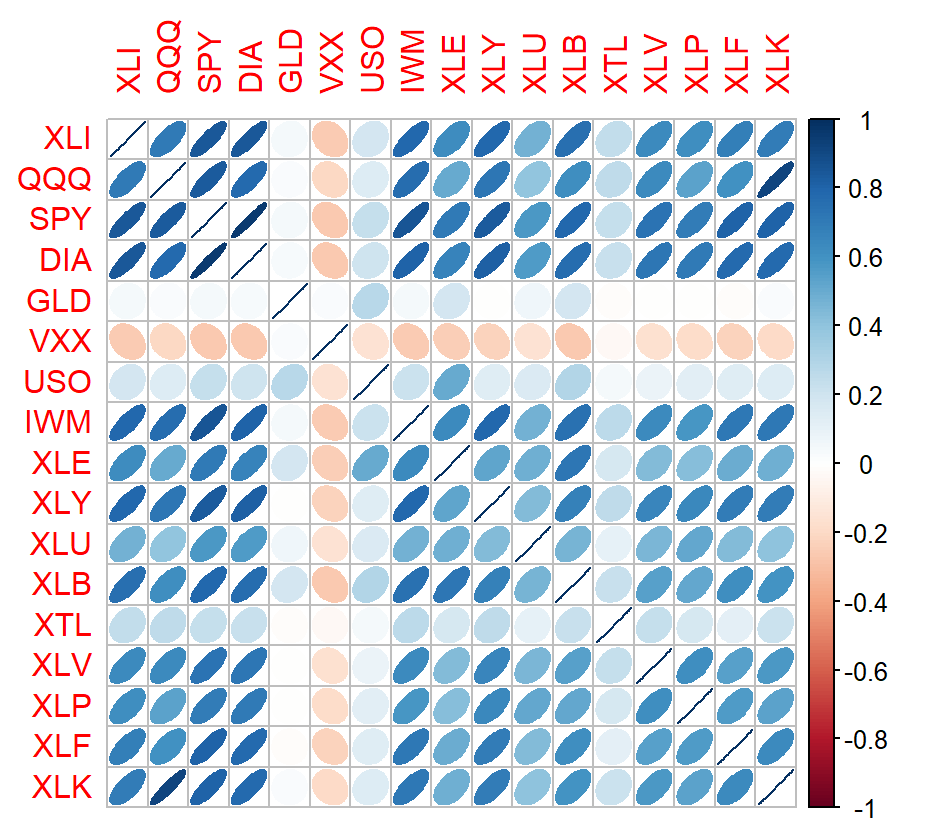
- 산점도
- 산점도가 교재와 다르게 나오는데 교재 이미지가 정사각형인 것을 보면 Python으로 코딩한 이미지인 듯함.
# scatterplot
telecom <- sp[, sp_s[sp_s$sector == 'telecommunications_services', 'symbol']]
telecom <- telecom[row.names(telecom) > '2012-07-01',]
plot(telecom$T, telecom$VZ, xlab = "AT", ylab = 'Verizon')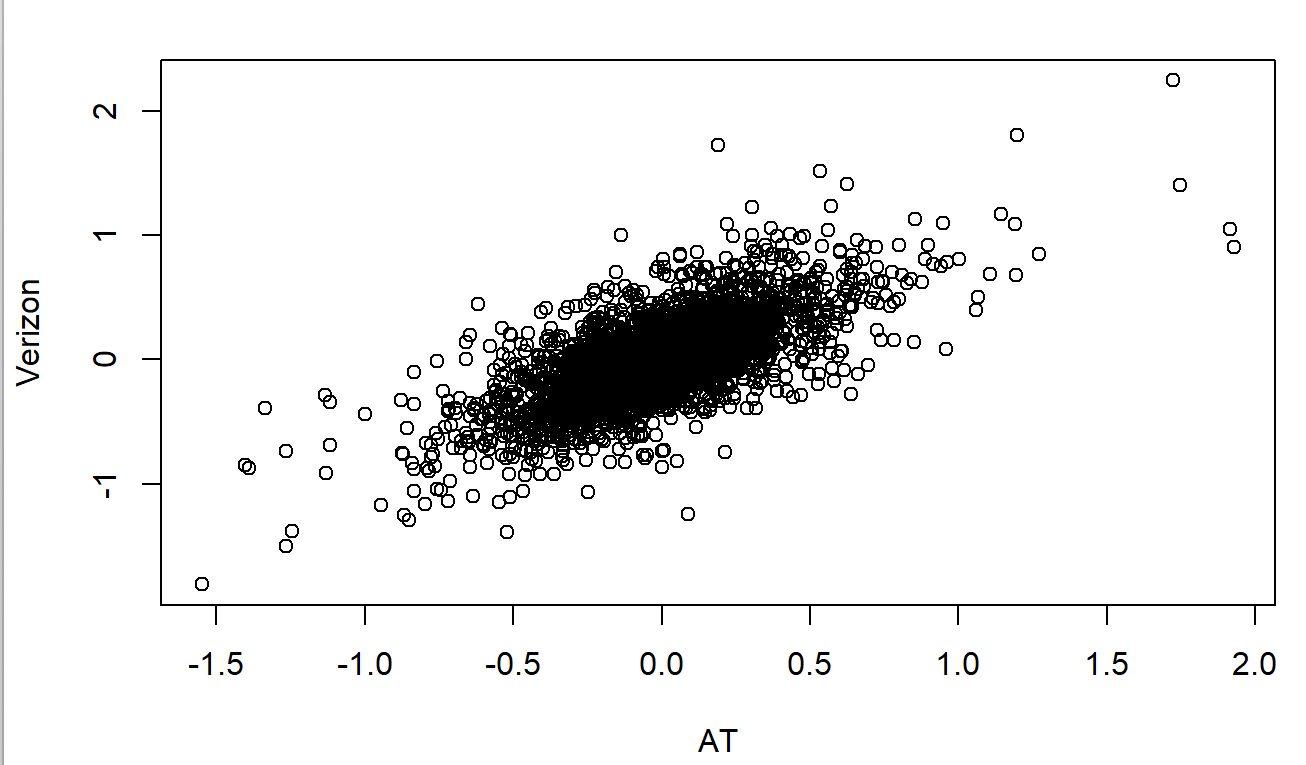
8. 두 개 이상의 변수 탐색
- 일변량분석 : 평균, 분산
- 이변량분석 : 상관분석
- 다변량분석
- 수치형 변수, 수치형 변수 : 육각형 구간, 등고선
- 현재 위치를 모르면 getwd()를 쓰면 됨.
- stat_binhex : 육각형 테두리 색상
- 등고선은 꽤 오래 걸림...;;
- 등고선이 밀집될수록 높은 지형이라는 것은 초등학교 때 배운 바 있음.
# hexagonal binning
route <- file.path(getwd())
tax <- read.csv(file.path(route, 'data', 'kc_tax.csv.gz'))
# 극단값 제거
tax <- subset(tax, TaxAssessedValue < 750000 &
SqFtTotLiving > 100 &
SqFtTotLiving < 3500)
nrow(tax)
#install.packages("ggplot2")
library(ggplot2)
graph1 <- ggplot(tax, (aes(x = SqFtTotLiving, y = TaxAssessedValue))) +
stat_binhex(color = 'gray') +
theme_bw() +
scale_fill_gradient(low = 'white', high = 'red') +
labs(x = "집 크기", y = "과세평가금액")
graph1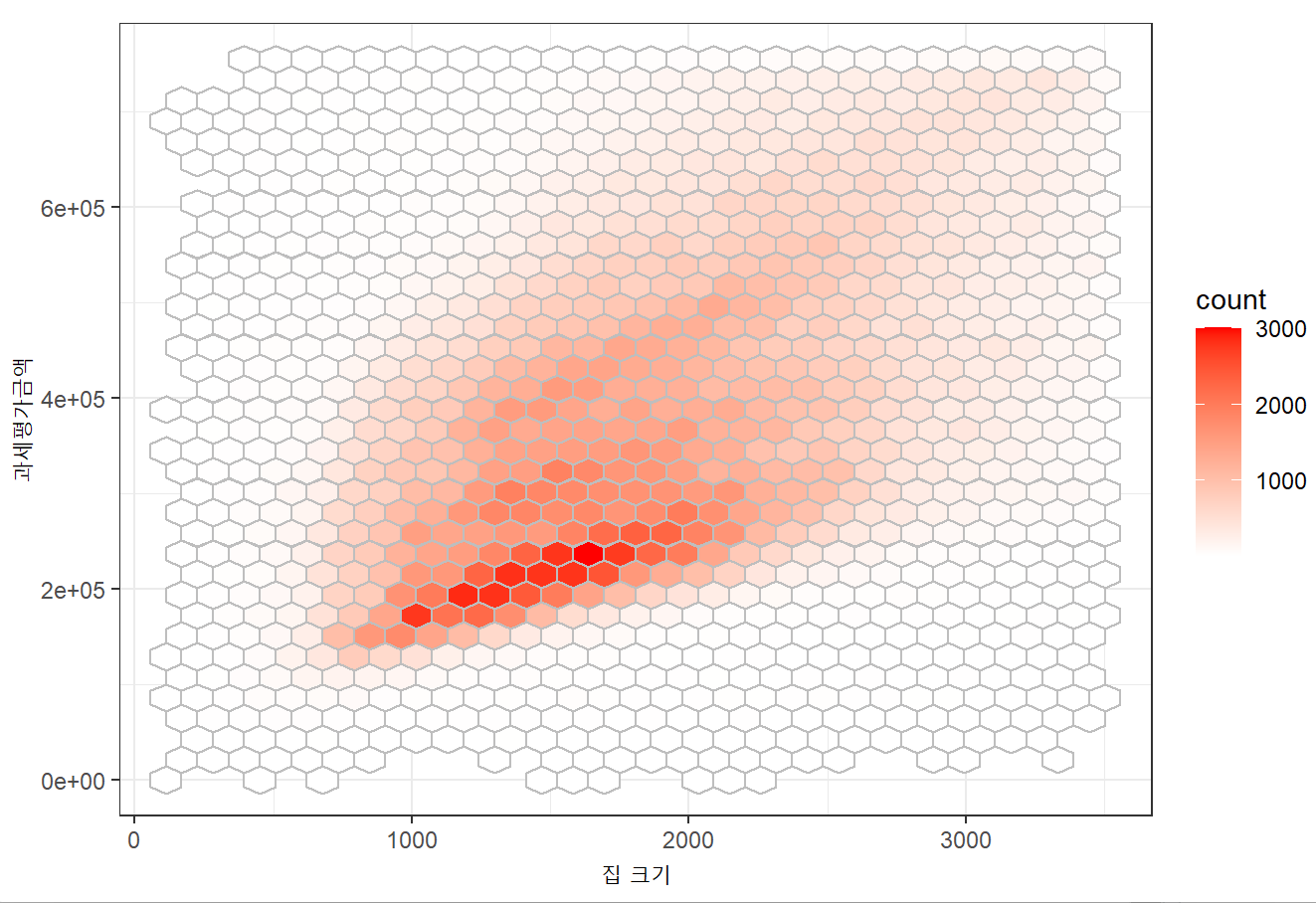
> # contours
> graph2 <- ggplot(tax, (aes(SqFtTotLiving, TaxAssessedValue))) +
+ theme_bw() +
+ geom_point(alpha = 0.07, color = 'red') +
+ geom_density2d(color = 'white') +
+ labs(x = "집 크기", y = "과세평가금액")
> graph2
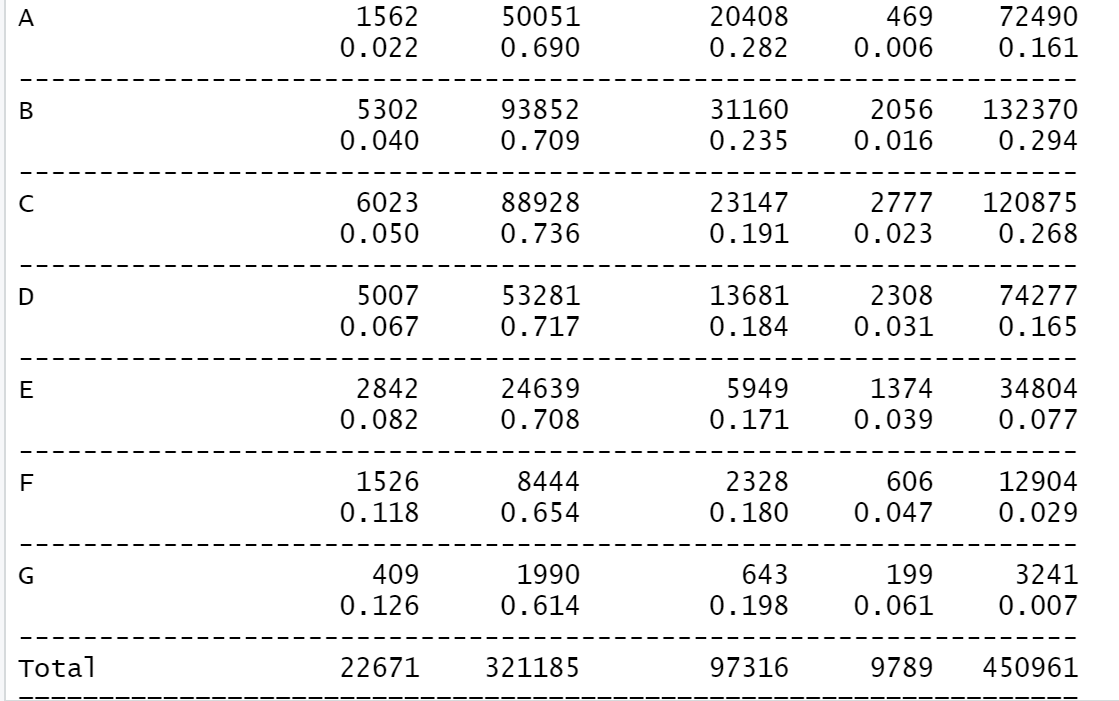
- 범주형, 범주형 : 분할표
- 대출등급과 대출 결과
# 분할표
route <- file.path(getwd())
loan <- read.csv(file.path(route, 'data', 'lc_loans.csv'))
#install.packages("descr")
library(descr)
CrossTable(loan$grade,loan$status,
prop.c = F, prop.chisq = F, prop.t =F)
- 범주형, 수치형 : 상자그림, 바이올린 도표
> # 상자그림
> as <- read.csv('./data/airline_stats.csv')
> boxplot(pct_carrier_delay ~ airline, data = as, ylim = c(0, 55))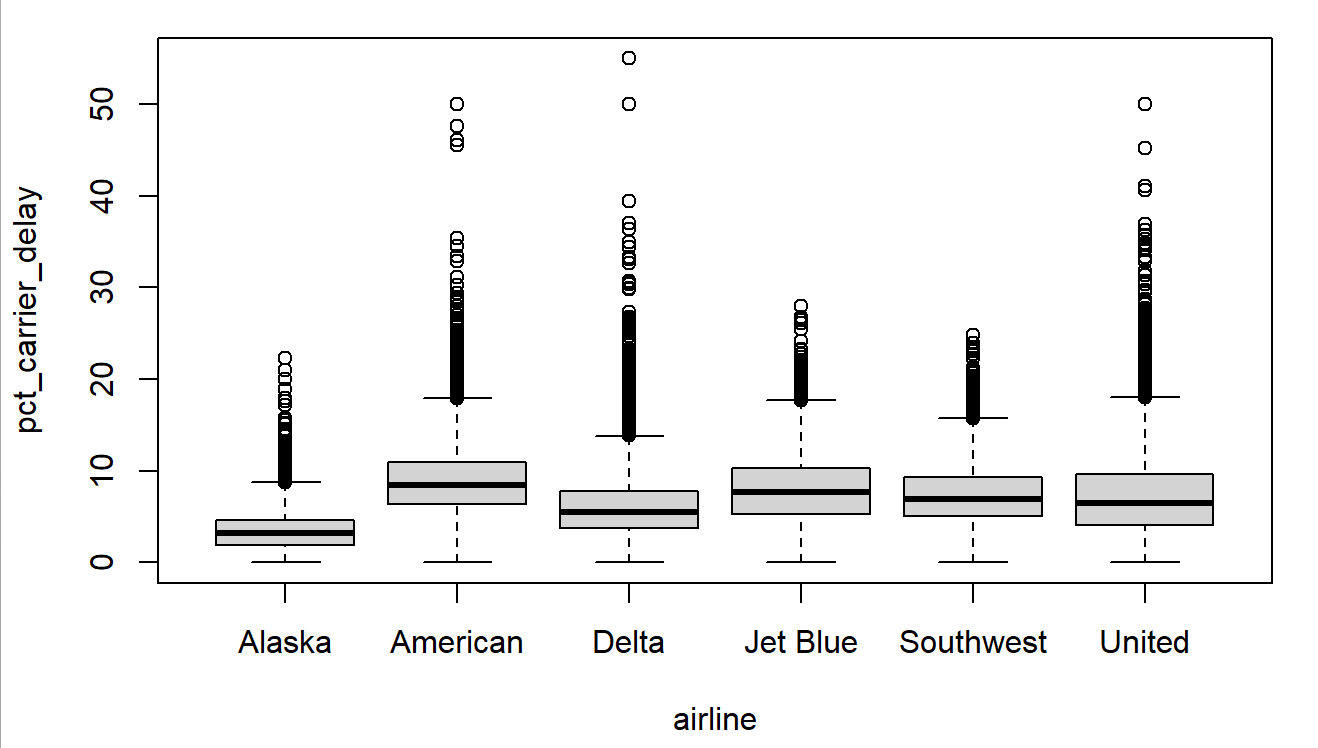
# 바이올린
ggplot(data = as, aes(airline, pct_carrier_delay)) +
ylim(0, 55) +
geom_violin() +
labs(x = '항공사', y = '일일 연착 비율')

- 다변수 시각화 : 조건화 활용
- facets : 조건화변수 (우편번호) 적용
# 조건화
ggplot(subset(tax, ZipCode %in% c(98188, 98108, 98107, 98125)),
aes(SqFtTotLiving, TaxAssessedValue)) +
stat_binhex(color = 'white') +
theme_bw() +
scale_fill_gradient(low = 'white', high = 'purple') +
labs(x = '집 크기', y= '과세평가금액') +
facet_wrap('ZipCode')
728x90
반응형
'Statistics > 데이터 과학을 위한 통계' 카테고리의 다른 글
| [Practical Statistics for Data Scientists] 3 - 통계적 실험과 유의성 검정 (0) | 2022.08.17 |
|---|---|
| [Practical Statistics for Data Scientists] 2 - 데이터와 표본분포 (0) | 2022.08.03 |

