[Practical Statistics for Data Scientists] 2 - 데이터와 표본분포

이전 글 : 2022.08.02 - [데이터/데이터 과학을 위한 통계] - [Practical Statistics for Data Scientists] 1 - 탐색적 데이터 분석 (EDA)

---

데이터의 질과 적합성을 일정 수준으로 담보할 수도 없으면서 데이터 크기만 늘어나는 것이 오늘날 상황이다.
- p.67, <Practicl Statistics for Data Scientists> -

---

 

  필자 역시 빅데이터를 활용하게 되어 표본조사에서 전수조사로 트렌드가 바뀜에 따라 표본추출이 덜 중요해질 것이라 생각했다. 그러나 오히려 데이터 편향의 최소화, 다양한 유형의 테스트를 위한 표본추출의 중요성이 더 증대되고 있다는 것이 저자들, 피터 브루스 외 2인의 의견이다. 'Practical Statistics for Data Scientists' 교재 67~107페이지의 내용을 공부하며 보다 효과적인 빅데이터 분석을 위한 토대를 쌓도록 하자.

<Practical Statistics for Data Scientists> 도서 페이지 : https://bit.ly/3zSetGu

---

 

Index

 

1. 임의표본추출과 표본편향

• 표본 : 큰 데이터 집단(모집단)에서 추출한 데이터의 부분집합.
• 임의표본추출 : 모집단에서 선택할 수 있는 원소들을 무작위로 추출하는 것
  • 단순임의표본 : 임의표본추출로 얻은 샘플
• 표본편향 : 모집단을 잘못 대표하는 표본
  • 자기선택 표본편향 : 리뷰 작성자들은 무작위로 선택된 것이 아니라 모종의 관련이 있는 사람들이라 편향된 평가를 하기 쉬움. 상황을 정확히 파악하기 위한 자료로 쓰기는 어려우나 비슷한 기관, 기업과 비교하는 것에는 도움이 됨. 즉, 하나의 개체에 대한 세밀한 분석용이 아닌 여러 개체와의 비교 분석에 리뷰가 도움이 된다는 뜻.
• 층화표본추출 : 모집단을 여러 층으로 나눠 각 층에서 랜덤하게 샘플을 추출하는 것 (제반요소를 고려해 특정 층에 가중치를 부여하기도 함.)
• 대량의 데이터가 필요한 경우? 큰 데이터 + 희소한 데이터
• 평균 기호
  • 모집단의 평균 : μ, 표본을 추론한 결과
  • 모집단의 표본평균 : xˉ, 관찰의 결과

2. 선택편향 

• 선택편향 : 데이터를 선택적으로 고르는 관습 때문에 생기는 편향
• 데이터 스누핑 : 광범위하게 데이터를 탐색하는 행위 (편향의 위험성 O)
• 평균으로의 회귀 : 이례적인 경우 관찰 ▶ 다음 실험에선 중간 정도의 케이스 관찰됨. 선택편향으로 나타나는 결과. (ex . Sophomore Jinx

3. 표본분포 

• 표본분포 : 동일한 모집단에서 취득한 여러 샘플 (표본)에 대한 표본통계량의 분포
• 표본통계량 : 모집단에서 도출된 표본으로 획득한 측정 지표
• 데이터 분포 ↔ 표본분포
  • 데이터 분포 : 데이터 개별값의 도수분포
  • 표본 분포 : 표본에서 얻은 표본통계량의 도수분포
•  중심극한정리 : 모집단이 정규분포가 아니더라도 표본크기가 충분하고 데이터가 정규성을 크게 이탈하지 않는다면 여러 표본에서 추출한 평균은 종 모양의 형태를 띤다.
  • 따라서 신뢰구간 및 가설검정 계산에 정규근사 공식 사용 가능 (ex. t-분포)

route <- file.path(getwd())

# libraries
library(ggplot2)

# data
data1 <- read.csv(file.path(route, 'data', 'loans_income.csv'))
# dataframe -> vector
data1 <- data1[,1]

# 단순임의표본
df1 <- data.frame(income = sample(data1, 1000),
                  type = 'dist')

# 5개값의 평균
df1_5 <- data.frame(income = tapply(sample(data1, 1000*5),
                                    rep(1:1000, rep(5,1000)),FUN = mean),
                    type = 'mean_of_5')

# 20개값의 평균
df1_20 <- data.frame(income = tapply(sample(data1, 1000*20),
                                    rep(1:1000, rep(20,1000)),FUN = mean),
                    type = 'mean_of_20')

# 바인딩 후 factor로 변환
income <- rbind(df1, df1_5, df1_20)
income$type = factor(income$type,
                     levels = c("dist", "mean_of_5", "mean_of_20"),
                     labels = c("Data", "mean of 5", "mean of 20"))

# 히스토그램 작성
ggplot(income, aes(x=income)) +
  geom_histogram(bins = 40) +
  facet_grid(type ~.)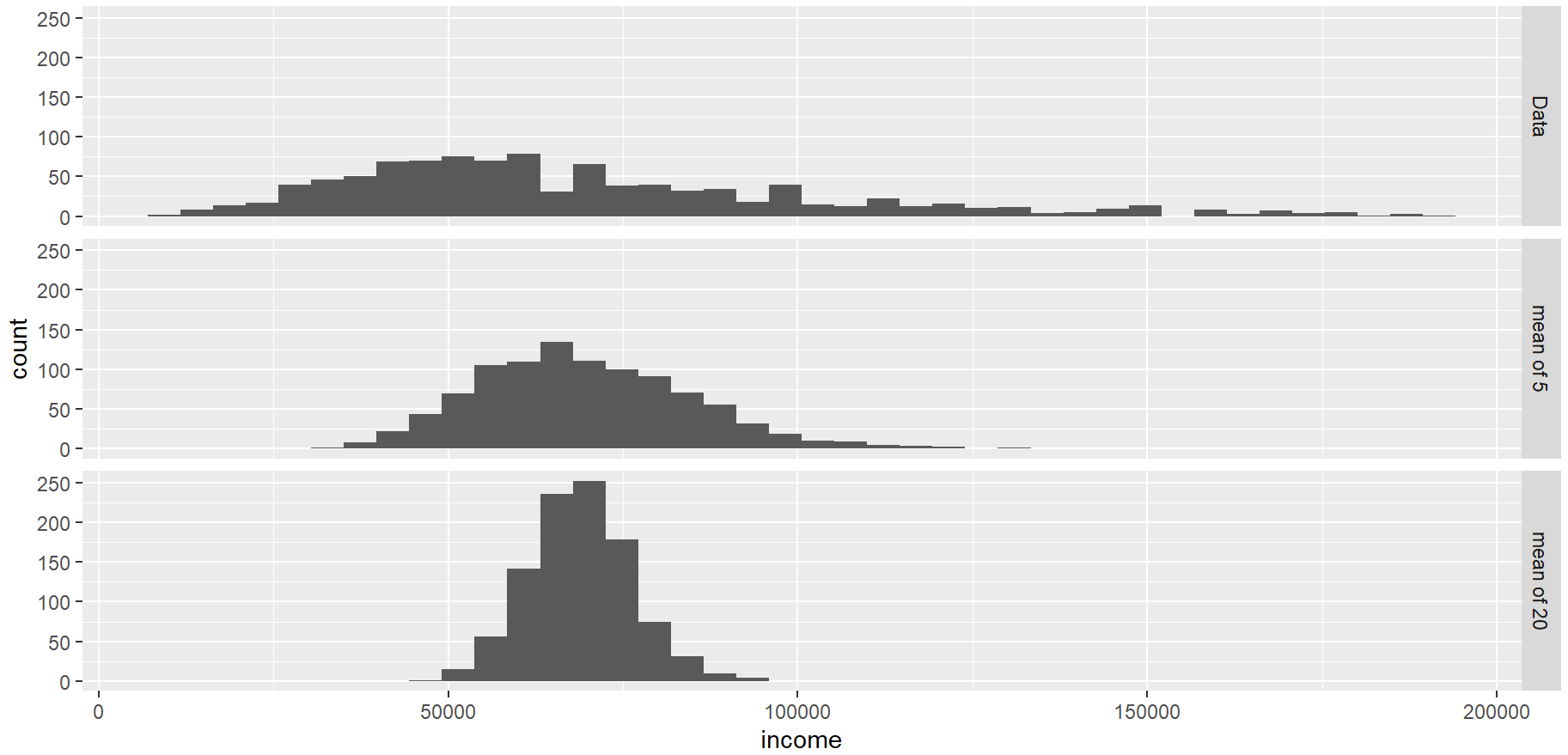

• 표준오차 : 표본분포의 변동성을 나타내는 단일 측정 지표.
  • SE = s (표준편차) / √n (표본크기)
  • 관계 : 표본크기가 커지면 표준오차 감소 (n제곱근의 법칙, 표준오차를 절반으로 줄이려면 표본크기 4배 증가)
• 표준편차 ↔ 표준오차
  • 개별 데이터와 표본 측정 지표의 변동성을 다룬다는 차이.

4. 부트스트랩

• 부트스트랩 : 현재 지닌 표본에서 추가적으로 표본을 복원추출하고 각 표본에 대한 통계량과 모델을 다시 계산하는 과정. 표본통계량의 변동성을 평가하는 강력한 도구.
• 부트스트랩 표본 : 관측 데이터 집합으로 얻은 복원추출 표본.
• 재표본추출 resampling : 관측 데이터를 반복해 표본추출하는 과정. 부트스트랩과 순열 절차를 거친다.
• 부트스트랩 재표본 추출 알고리즘
  • 1) 샘플을 하나 뽑아 기록 후 제자리에
  • 2) n번 반복
  • 3) 재표본추출된 값의 평균 확인
  • 4) 위의 과정을 R번 반복.
  • 5) R개의 결과로 표준편차 (표본평균의 표준오차) 계산, 히스토그램 및 상자그림으로 시각화, 신뢰구간 도출.
• R 코드
  • 중앙값 추정지 : 62k 달러 / 편향 : 추정치에서 -70불 / 표준오차 : 약 209불

> # Bootstrap_220815
> library(boot)
> # idx로 지정된 표본의 중앙값 계산
> stat_fun <- function(x, idx) median(x[idx])
> boot_obj <- boot(data1, R = 1000, statistic=stat_fun)
> boot_obj

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = data1, statistic = stat_fun, R = 1000)


Bootstrap Statistics :
    original   bias    std. error
t1*    62000 -72.6925    214.3206

 

• 배깅 : 분류 및 회귀 트리 사용 시, 여러 부트스트램 샘플로 트리를 여러 개 만들고, 각 트리에서 나온 예측값의 평균을 구하는 것. (여러 부트스트랩 표본으로 얻은 예측값으로 결론을 만드는 것)

※ 부트스트랩은 표본크기가 작은 것을 보완하기 위한 것이 아님. 모집단에서 추가로 표본을 뽑는다고 할 때, 그 표본이 원 표본과 비슷한지를 알려주는 기능.

• 재표본추출 ↔ 부트스트래핑 
  • 재표본추출 : 여러 표본이 결합돼 비복원추출을 실히할 수 있는 순열 과정 포함.
  • 부트스트랩 : 항상 관측된 데이터로부터 복원추출

5. 신뢰구간

도수분포표, 히스토그램, 상자그램, 표준오차는 표본추정에서 잠재적 오차를 살펴보는 방법. but 신뢰구간은 다름.

• 신뢰수준 confidence level : 동일 모집단에서 같은 방식으로 얻은 관심 통게량을 포함할 것으로 예상되는 신뢰구간의 백분율
• 구간끝점 interval endpoint : 신뢰구간의 최상, 최하위 포인트
• 예시 : 95%의 신뢰구간 - 표본통계량의 부트스트랩 표본분포 90%를 포함하는 구간.
• 부트스트랩 신뢰구간 도출 방법
  • 1) 재표본추출
  • 2) 1번 단계에서 구한 표본에 대해 원하는 통계량 기록
  • 3) 1, 2번 단계를 R번 반복
  • 4) x% 신뢰구간을 구하고자 R개의 재표본 결과의 분포 양쪽 끝에서 (100-x)/2%만큼 제거
  • 5) 절단한 점은 x% 부트스트랩 신뢰구간의 양 끝점.

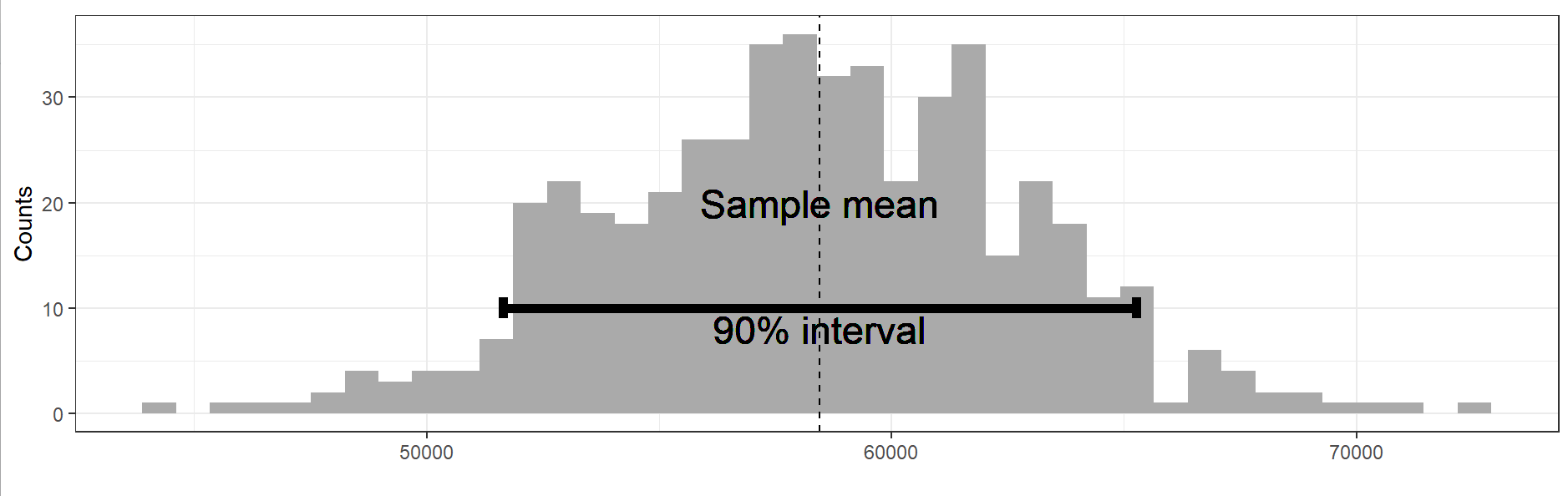
6. 정규분포

• 용어 정리
  • 정규분포 : 표본통계량 분포가 일정한 모양이 있음.
  • 오차 : 데이터 포인트와 예측값 혹은 평균 간의 차
  • 표준화(정규화)하다 standardize : 평균을 빼고 표준편차로 나눔.
  • z-점수 : 각 데이터 포인트를 정규화한 것
  • 표준정규분포 : 평균 = 0, 표준편차 = 1인 정규분포
  • QQ plot : 표본분포가 특정 분포 (정규분포 등)에 얼마나 가까운지 시각화한 그림
• 표준정규분포 : x축 단위가 평균의 표준편차로 나타나는 정규분포.

> nor_sam <- rnorm(100)
> qqnorm(nor_sam)
> abline(a = 0, b= 1, col = 'green')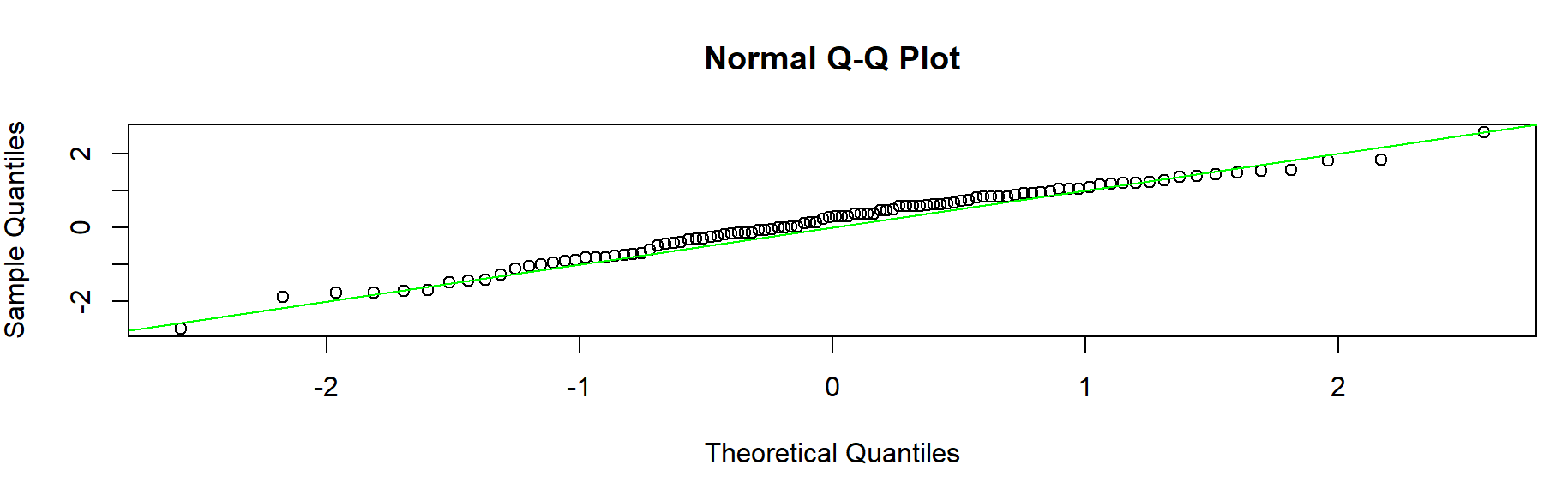

표준정규분포에서 추출한 100개 표본의 QQ Plot

 

• 데이터를 z 점수로 변환하기 위해 데이터 값에서 평균을 빼고 표준편차로 나눔. ☞ 정규분포와 비교 가능해짐. (데이터가 정규분포가 되는 것은 아님)

7. 긴 꼬리 분포

정규 normal 라는 이름과 달리 데이터는 일반적으로 정규분포를 띠지 않는다.

• 용어 정리
  • 왜도 skewness : 분포의 한쪽 꼬리가 반대쪽보다 긴  정도
• 분포의 꼬리는 양 극한값에 해당. 
• 실무에서는 긴 꼬리를 주시하는 것이 중요. (ex. black swan theory)

> # long tail distribution
> ## load data
> sp500 <- read.csv(file.path(route, 'data', 'sp500_data.csv.gz'), row.names=1)
> nf <- sp500[, 'NFLX']
> nf <- diff(log(nf[nf>0]))
> qqnorm(nf)
> abline(a=0, b=1, col='red')

 

QQ Plot - 넷플릭스 일일 주식 수익률

 

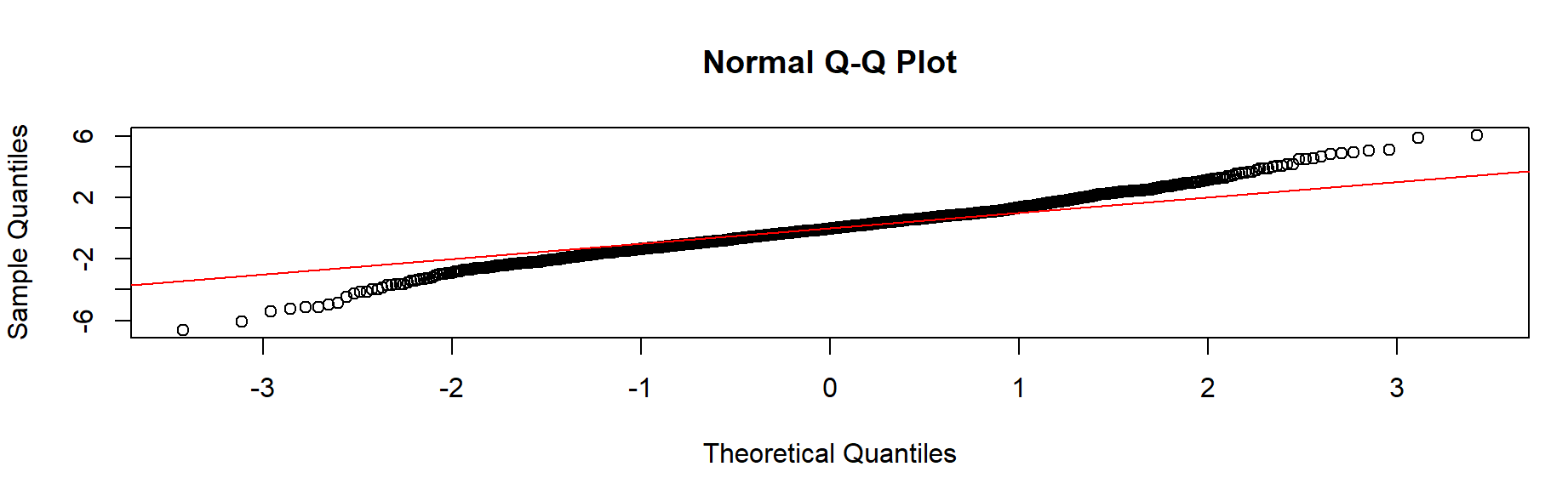
• 넷플릭스 QQ Plot은 6절의 QQ 그림에 비해 대각선과 일치하지 않는 경향을 보인다. ☞ 정규분포를 따르지 않음.
• 평균에서 표준편차 이내의 데이터 포인트는 선과 가까움 ☞ 중간에서는 정상 + 긴 꼬리 by Tukey

8. 스튜던트의 t 분포 

t-분포는 정규분포와 형태가 유사하나 꼬리부분이 더 두껍고 긺. 표본통계량의 분포를 설명하는 데 활용.

• 용어 정리
  • 자유도 degrees of freedom : 다른 표본크기, 통계량, 그룹의 수에 따라 t-분포를 조절하는 변수
• 윌리엄 고셋 (기네스 근무)의 연구에서 기인함.
• 모집단이 정규분포를 따르지 않을 떄도 표본통계량은 대개 정규분포를 따름 (중심극한정리) ☞ t-분포가 널리 사용됨.
• t 분포는 표본평균, 두 표본평균의 차, 회귀 파라미터 등의 분포를 위한 기준으로 활용됨.

9. 이항분포

이항식 (yes or no)의 결론은 의사 결정 과정에서 중요.

• 일련의 시행은 정해진 확률로 2가지 결과를 지님.
• 용어 정리
  • 시행 : 독립된 결과를 가져오는 하나의 사건 (ex. 야구에서 출루 or 아웃)
  • 성공 : 시행에 대한 관심의 결과 (유의어 : 1)
  • 이항식 binomial : 두 가지 결과를 가짐.
  • 이항시행 : 두가지 결과를 초래하는 시행 (유의어 : 베르누이 시행)
  • 이항분포 : n번 시행에서 성공한 횟수에 대한 분포 (유의어 : 베르누이 분포)
• 성공확률 : p, 시행 횟수 : n일 때, 평균은 n * p, 분산은 n * p * (1-p)
• n이 크고 p가 0이나 1에 지나치게 가깝지 않다면 정규분포로 근사할 수 있다.
• dbinom : 5회 시행, 2회 성공, 성공률 0.1 / pbinom : 성공률 : 0.1, 시행 : 5회일 때, 2회 이하의 성공 확률.

> dbinom(x=2, size=5, p=0.1)
[1] 0.0729
> pbinom(2, 5, 0.1)
[1] 0.99144

10. 카이제곱 분포

• 통계학에서 범주의 수에 대해 기댓값에서 이탈한다는 개념이 중요.
• 기댓값 : 데이터에서 특이하거나 주목할 만한 것이 없다. ▶ 귀무가설 (귀무모델)
• 카이제곱 통계량 : 검정 결과가 독립성에 대한 귀무 기댓값에서 벗어난 정도를 측정하는 통계량. (관측값과 기댓값의 차이 / 기댓값의 제곱근)^2 후, 모든 범주에 대해 합산.
• 카이제곱 통계량은 관측 데이터가 특정분포에 적합한 정도를 나타냄.
• 카이제곱 분포 : 귀무 모델에서 반복적으로 재표본추출한 통계량 분포. 

11. F 분포

• 여러 그룹에 걸쳐 서로 다른 처리를 테스트할 때 쓰임.
• 각 그룹 내 변동성 (잔차 변동성)에 대한 그룹 평균간 변동성의 비율 ☞ 이러한 비교를 분산분석 ANOVA 이라고 함.
• F 통계량의 분포 : 모든 그룹의 평균이 동일할 때 (귀무모델), 무작위 순열 데이터로 생성되는 모든 값의 빈도 분포.
• 회귀 모형에 의해 설명된 변동성을 데이터 전체의 변동과 비교하고자 선형회귀에도 활용됨.
• F 분포는 측정된 데이터와 관련한 실험 및 선형 모델에 활용.
• F 통계량은 관시 요인으로 인한 변동성과 전체 변동성 비교.

12. 푸아송 분포와 기타 분포

대부분의 작업이 주어진 비율에 따라 임의로 사건 발생. (ex. 1제곱미터당 건물의 결함, 100페이지 당 오타 등)

• 용어 정리
  • 람다 lambda : 단위 시간이나 면적 당 사건이 발생하는 비율
  • 푸아송 분포 Poisson distribution : 표집된 단위 시간 혹은 공간에서 발생한 사건의 도수분포
  • 지수분포 exponential distribution : 한 사건에서 다음 사건까지의 시간이나 거리에 대한 도수분포
  • 베이불 분포 Weibull distribution : 사건 발생율이 시간에 따라 변화하는 지수분포의 일반화 버전
• 푸아송 분포
  • 예시 : 1시간동안 공항에 도착한 짐을 95%의 확률로 완벽히 처리하는데 필요한 노동력은 얼마인가?
  • 핵심 파라미터 : 람다 ☞ 분산도 람다
  • R 코드 : 1분당 평균 5회로 챗봇이 답변한다면, 100분으로 가정해 100분당 챗봇 답변 횟수를 제시 

# poisson
> rpois(100, lambda = 5)
  [1]  3  5  3  6  6  5  6  9  9  3  5  6  5
 [14] 11  4  9 12  5  7  4  3  3  3  3  7  8
 [27]  6  2  4 10  9  4  7  4  1  5  1  4  7
 [40]  9  6  4  8  9  9  2  6  6  5  4  2  5
 [53]  6  8  4  3  7  6  7  8  6  6  6  4  4
 [66]  4  3  5  7  4  8  1  7  4  5  3  7  6
 [79]  7  0  6  3  5  5  8  2  5  3  5  7  3
 [92]  4  6  5  6  3  8  2  7 11

• 지수분포
  • 변수 람다를 사용해 사건과 사건 사이의 시간 분포를 모델링
  • 예시 : 고장이 발생하는 시간, C/S처리에 걸리는 시간 등
  • R 코드 : 분당 평균 0.05회 댓글이 달릴 때, 100분 동안의 페이지 댓글 가정

 # exponential
> rexp(n =100, rate = 0.05)
  [1]  1.02737798  2.41573480  1.40328017
  [4] 18.43378294 28.27627253  3.57263341
  [7] 31.40445184  1.21013406  1.14263286
 [10] 22.71732892 18.36380688 30.22526972
 [13] 17.60293418 37.40118760 79.99398361
 [16] 31.74766578 21.49274150  6.83272550
 [19] 53.31309560  0.43278974 12.40991767
 [22] 96.31781436 47.82245453 10.26364564
 [25] 12.63744279 75.27082692 30.50691917
 [28]  0.65093112 32.21604392  1.58100092
 [31]  8.31920973 18.50532947  5.66618104
 [34]  1.71431933 16.20633092  3.60384462
 [37] 24.02102653 12.06633278 13.72806003
 [40] 18.88881987  7.58063075 10.05224743
 [43] 45.64405862  9.73160692 29.40644133
 [46]  2.27651684 15.84623948  2.37021861
 [49]  4.12368981 14.18636251 12.57734412
 [52] 24.74666120 32.02553395  2.92690987
 [55] 37.40498520 33.76597626 28.36094917
 [58] 30.92949793 23.82145274 26.33244272
 [61]  3.41229318  0.05018859 35.65349102
 [64] 12.45847469  7.16726665 37.18965963
 [67] 57.32579797  2.20660574  3.77072764
 [70] 39.81835317  1.13383664  2.69245254
 [73] 64.33451175 15.61958503  7.65497210
 [76] 38.99054203  3.97033362 17.02565809
 [79]  6.23711508 23.89427593  0.74594965
 [82]  4.72229902  3.71269765  0.82851935
 [85] 12.03893213 17.35894398  0.98426991
 [88] 11.46021237 16.71259599 10.58229492
 [91]  4.73438698 28.01695846 61.82607114
 [94] 14.26107595  2.50155567 12.45595018
 [97] 13.68525832 16.54985525  7.04046740
[100] 11.60273767

• 고장률 추정
  • 사건발생 비율 람다는 이미 파악됐거나 기존 데이터로 추정할 수 있으나 드물게 일어나는 사건에 한해서는 람다를 구하기 어려움. ☞ 적합도 검정 활용
• 베이불 분포
  • 대다수의 경우, 사건 발생률은 시간에 따라 일정치 않음. ☞ 지수 or 푸아송 분포가 유효하지 않음. (ex. 시간의 흐름에 따라 건물에 이상이 있을 확률이 올라감)
  • 베이불 분포 : 지수분포를 확장한 것. 형상 파라미터 베타를 지정해 달라진 발생률 적용 가능.
  • 에타 : 척도 변수. 고장 시간 분석에 사용되므로 특성 수명으로 표현됨.
  • R 코드 : 1.25의 형상 파라미터&5,000의 특성수명을 지닌 베이불 분포에서 난수 100개(수명) 생성 (형상 파라미터가 1보다 크면 발생률은 점점 증가한다.)

 # Weibull
> rweibull(100, 1.25, 5000)
  [1]  8619.6388  5160.7825  2723.0711
  [4]  5099.6530  3181.3779  8912.8141
  [7]  3342.5714  2811.0453  3530.6412
 [10]  6655.3002  2150.0555 14370.9240
 [13]  9292.5278  5239.2682  4448.4715
 [16]  2232.7476  5920.1436  1396.6311
 [19]  4421.3145  2477.0476  9291.2972
 [22]  6051.6480  1538.6567  2448.8619
 [25]  4169.2879  5906.0662  3721.3032
 [28]  2880.0624  5886.5088  7030.0237
 [31]  6164.1159  4994.1982  9979.2895
 [34]  4944.1038  4840.6326 15242.6529
 [37]  3690.3756  3990.6872 10205.7481
 [40]  1014.1844  2660.1163  3537.3755
 [43]  2163.9784   837.8681  2956.0748
 [46]  2966.8687  2460.1094  5402.2408
 [49]  3738.4958  4425.1089  2159.1608
 [52]  3513.9968  1906.0849 10577.6217
 [55]   534.6009  3878.0125  4185.2315
 [58] 16150.8654  4079.3620  4829.4761
 [61]  4800.2336  3798.8261  4108.4334
 [64]  3288.7212   345.0497  3231.0409
 [67]  2225.0685  2555.8629  4318.8260
 [70]  3243.0732  3967.7374  4596.4038
 [73]  5214.2702  8334.3521  3005.7480
 [76]  9922.2898  2559.4258  2750.1850
 [79]  2003.8078  1747.7743  1014.9232
 [82]  7580.9984  8824.0852  8555.3639
 [85]  1506.6385  3362.5709   887.7343
 [88] 13799.2943  4524.3995  3291.5725
 [91]  2341.3306  7086.6292  6474.9787
 [94]  3066.6433  3849.8627 10897.7567
 [97]  4428.5998  2079.1992  2716.2388
[100]  5797.3375